| 1) PUNTOS FIJOS DE UNA FUNCIÓN |
En esta sección vamos a introducir el concepto de "puntos fijos de una función", concepto que nos permitirá comprender mejor la resolución iterativa de ecuaciones así como extender la misma a ecuaciones un poco más complejas.
Un punto "c" se dice que es fijo para la función f si se cumple que f(c) = c, es decir, si la imagen de c coincide con c. Gráficamente, un punto fijo no es otra cosa que el punto de corte de la gráfica de la función f(x) con la recta y = x. Puedes ver a continuación algunos
|
En la siguiene escena puedes introducir la función que quieras en el cuadro de texto de la parte inferior, haz coincidir los puntos azul y rojo y tendrás una aproximación de los puntos fijos de dicha función:
|
| |
| |
| 2) CALCULO ITERATIVO DE LOS PUNTOS FIJOS DE UNA FUNCIÓN. RESOLUCIÓN DE ECUACIONES. |
Supongamos que queremos resolver la ecuación x - 1 = cosx. Esta ecuación ya no es tan sencilla de resolver como las de primer y segundo grado que veíamos anteriormente. Pero todavía tenemos una esperanza. Pongamos la ecuación en esta otra forma:
x = 1 + cosx
De este modo el problema se reduce a obtener el punto, o puntos, fijos de la función f(x) = 1 + cosx, es decir el punto, o puntos de corte de dicha función con la recta f(x) = x. En la siguiente escena vamos a calcular de forma iterativa el valor de dicho punto. Para ello, aumenta el control "iter" y observa los valores de cada nueva aproximación; cuando la diferencia entre las dos últimas aproximaciones sea menor o igual que la precisión deseada, tendrás una solución, aproximada según dicha precisión claro, de la solución de la ecuación. La escena te avisará cuando la precisión sea de una centésima:
|
| |
Cabe preguntarse si puede utilizarse este método para resolver cualquier ecuación. La respuesta es no, como puedes comprobar intentando resolver la ecuación x = 10x - 2 . Pon el segundo miembro de esta ecuación en el campo correspondiente a f y prueba con una primera aproximación x0 = 0.5 para aproximar el punto fijo de abscisa positiva. Verás que las sucesión de valores xn va creciendo indefinidamente, es decir no converge a ningún valor real. Sin embargo, esta ecuación puede escribirse de otra forma tomando logaritmos:
x + 2 = 10x → x = log (x + 2)
|
Escribe ahora log(x+2) en el campo correspondiente a f y observa que bastan 4 iteraciones para conseguir una aproximación de la solución a las centésimas. Por consiguiente todo parece indicar que la convergencia depende de la forma de la función f(x). ¿Cuál es la forma, o qué condiciones tiene que cumplir la función f(x)? Veremos la respuesta en la siguiente sección (funciones contractivas), donde resolveremos todas las cuestiones pendientes. Pero antes, para practicar, intenta resolver las siguientes ecuaciones con una precisión a las centésimas por lo menos:
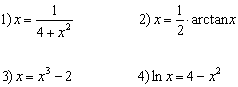
|
| |
 |
Indice |
Aplicaciones contractivas
|
|


