| 1) APLICACIONES CONTRACTIVAS |
Como veíamos en el apartado anterior, el éxito del método de iteraciones para la resolución de una ecuación depende de la forma de la función f(x) empleada para ello. En este, y los siguientes apartados, vamos a estudiar el concepto de aplicación contractiva que nos sacará de dudas sobre este tema y nos resolverá todas las cuestiones pendientes.
Una función
f : R → R
es contractiva si existe una constante k < 1 tal que para cualesquiera
x1, x2 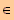 R se cumple: R se cumple:
d( f(x1), f(x2)) < k . d(x1, x2)
Es decir, una aplicación contractiva es aquella que contrae las distancias con una razón de contracción estrictamente menor que la unidad. Recuerda que, en el conjunto de los números reales, se define la distancia entre dos de ellos de la siguiente forma:
d(x1, x2) = | x1- x2 |
por lo que la definición de aplicación contractiva queda del siguiente modo:
| f (x1) - f (x2) | < k . | x1- x2 |
Veamos algunos ejemplos de funciones contractivas. En la siguiente escena varía a tu gusto los valores de x1 y de x2 y observa en cada caso cómo se contraen las distancias. Puedes acceder también a una demostración con más rigor:
|
| |
| |
| 2) TEOREMA DE LA FUNCIÓN CONTRACTIVA O DEL PUNTO FIJO |
La verdadera utilidad de las funciones contractivas en el tema que nos ocupa, reside en el siguiente teorema:
Si una función
f(x) : [a, b] →[a, b] es contractiva, entonces tiene un único punto fijo x en el intervalo [a,b] y dicho punto se obtiene mediante el límite:
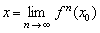
|
Este hecho explica bastantes cosas. Pensemos, por ejemplo, en el caso de la resolución de ecuaciones de primer grado, su escena era la siuiente:
|
|
Para resolver la ecuación ax + b = cx + d podemos comenzar a iterar tomando ax0 + b (elegimos f(x) en el control "recta") y luego vamos horizontalmente hasta encontrarnos con la recta roja ( g(x) = cx + d ) para obtener x1 = (ax0 + b - d).c-1 y repetir el proceso (mediante el control "iter" ) . Efectivamente, esto es equivalente a resolver la ecuación:

|
Por tanto, el proceso iterativo tendrá garantizada su convergencia, de acuerdo con el teorema anterior, si la función:
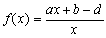
es contractiva. Pon aquí la función que resulte y haz tus conjeturas. ¿Cuándo es contractiva la función f(x)? Aquí tienes la
|
Como ves, la función f(x) será contractiva cuando |a| < |c|, es decir cuando la pendiente de la recta en la que comenzamos las iteraciones ( ax + b tiene pendiente a ) sea, en valor absoluto, menor estrictamente que la pendiente de la recta sobre la que vamos luego horizontamente ( cx + d tiene pendiente c ). Por consiguiente, en el ejemplo de la escena, como |a| = 1 es menor que |c| = 2, f(x) es contractiva en todo el conjunto de los números reales y cualquiera que sea la primera aproximación x0 elegida nos llevará, en el límite, a la solución de la ecuación de forma tan aproximada como queramos. Sin embargo, si eliges g(x) en el control "recta" , es decir si empezamos a iterar en la recta cx + d para luego ir horizontalmente sobre la recta ax + b, tomamos cx0 + d y luego vamos horizontalmente hasta la recta verde para obtener x1 = (cx0 + d - b).a-1 como siguiente aproximación, es decir en este caso estamos intentando resolver la ecuación:
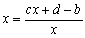
|
Pero en el ejemplo de la escena, ejemplo que luego tú puedes cambiar, la pendiente c de la recta cx + d es mayor en valor absoluto que la pendiente a de la recta ax + b, por lo que la función:
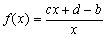
no es contractiva y el éxito del método iterativo no está garantizado, de hecho, como puedes comprobar en la escena, los sucesivos valores de xn divergen.
Ahora puedes comprender también, como caso particular, cuándo un mercado será estable y cuando no. Razona la respuesta con ayuda de los comentarios anteriores.
|
| |
| |
| 3) UNA CARACTERIZACIÓN DE LAS FUNCIONES CONTRACTIVAS. TEOREMA DEL VALOR MEDIO |
No simpre es fácil encontrar una demostración de que una función es contractiva. En este apartado vamos a estudiar una caracterización de función contractiva basada en el conocido teorema del valor medio de Lagrange. Empecemos pues:
TEOREMA DEL VALOR MEDIO Si una función f(x) es derivable en un intervalo (a ,b) entonces existe un punto x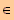 (a ,b) tal que se cumple: (a ,b) tal que se cumple:
f(b) - f(a) = f ' (x).(b - a)
|
En la siguiente
tienes una interpretación gráfica de este teorema |
Ahora, estamos en condiciones de enunciar el siguiente resultado:
TEOREMA. CARACTERIZACIÓN DE LAS FUNCIONES CONTRACTIVAS
Si una función f(x) es derivable en un intervalo [a ,b] y tal que | f ' (x) | < k < 1 para cualquier
x 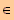 [a ,b], entonces f(x) es contractiva con constante de contracción k en el intervalo [a ,b]. La demostración de este teorema es muy sencilla con la ayuda del teorema del valor medio. Efectivamente, si x1 y x2 son dos elementos del intervalo [a ,b], se tiene:
[a ,b], entonces f(x) es contractiva con constante de contracción k en el intervalo [a ,b]. La demostración de este teorema es muy sencilla con la ayuda del teorema del valor medio. Efectivamente, si x1 y x2 son dos elementos del intervalo [a ,b], se tiene:
| f (x1) - f (x2) | = | f ' (x) | . | x1- x2 | < k . | x1- x2 |
|
El primer paso está garantizado por el teorema del valor medio y el segundo por las hipótesis del teorema de caracterización. |
¿Por qué es importante este teorema? Pensemos en el método utilizado para aproximar raíces, ¿lo recuerdas? Échale un vistazo al
Por ejemplo, la escena que utilizábamos para ilustrarlo, aproximando la raíz cuadrada de 3, era la siguiente:
|
Como puedes observar, este método es equivalente a resolver la ecuación:
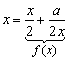
|
Pon aquí la función
f(x) con el valor de "a" que quieras, 3 por ejemplo, y observa lo rápido que converge si se elige x0 adecuadamente. Y es que, según el teorema anterior, se tiene:
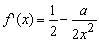
|
Por tanto, si
x >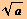 se tendrá: se tendrá:
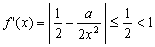
|
Por tanto la función es contractiva en el intervalo
(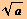 ,
∞)
y si elegimos la primera iteración x0 en dicho intervalo, según el teorema de la función contractiva, la convergencia está asegurada. Lo más cómodo es tomar como primera aproximación el menor número entero mayor que
la raíz de a
. Por ejemplo, para la raíz de 3, tomábamos x0 = 2. ,
∞)
y si elegimos la primera iteración x0 en dicho intervalo, según el teorema de la función contractiva, la convergencia está asegurada. Lo más cómodo es tomar como primera aproximación el menor número entero mayor que
la raíz de a
. Por ejemplo, para la raíz de 3, tomábamos x0 = 2.
|
| |
|
Indice |


