Límites laterales de un punto

	LÍMITES LATERALES EN UN PUNTO
	Análisis

1. LÍMITES LATERALES EN UN PUNTO

Ya hemos visto, en el apartado anterior, que se entiende por límite de una función en un punto. A partir de la idea de límite, vamos a ver a continuación como se define el límite lateral por la izquierda y el límite lateral por la derecha de una función en un punto.

En las siguientes escenas tienes representadas dos funciones reales de variable real. Con el controlador de nombre epsilon puedes modificar el valor de ε y se cambiará la longitud de intervalo correspondiente. El controlador de nombre Límites Laterales hace referencia al límite lateral por la izquierda y al límite lateral por la derecha, respectivamente.

Ejemplo 1

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Selecciona algún valor del controlador Límites Laterales. Verás que nos aparece en los ejes de coordenadas dos segmentos, uno de color verde de centro L y otro de color rojo de centro el punto a. Dentro del segmento rojo nos aparece también el punto x, el cual se puede desplazar a lo largo del segmento.

Si cambias el valor de epsilón, verás que el tamaño de los segmentos varía. Lo interesante es que, sea cual sea el valor que tome epsilón, el punto x siempre está dentro del segmento de color rojo y a su vez,

se mantiene dentro del segmento verde.

1.- Selecciona el valor 1 del controlador de Límites Laterales, que se corresponde con el Límite lateral por la derecha de la función en el punto a. Si aproximamos x a a, ¿hacia dónde tiende el punto

?

2.- Selecciona ahora el valor 2, que se correponde con el Límite lateral por la izquierda de la función en el punto a. Si hacemos tender el punto x a a, ¿hacia dónde se aproxima

?

3.- Por último, selecciona el valor 3 del controlador. En este caso, si movemos el punto x hacia a, ¿que ocurre con

Ejemplo 2

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

4.- Responde de nuevo las tres preguntas anteriores aplicadas a este caso.

Definición de los límites laterales en un punto

En respuesta a la primera pregunta diremos que el número real L es el límite lateral por la derecha de la función

. Para la segunda pregunta planteada, diremos que el número real L es el límite lateral por la izquierda de la función

Formalmente diremos que:

Un número real L, es el límite lateral por la izquierda de una función , en un punto a , si, al tomar valores de x suficientemente próximos a a, con x < a, los valores de las imágenes, , están tan próximas a L , como se desee. Se designa por:
De forma análoga, un número real L, es el límite lateral por la derecha de una función , en un punto, a , si al tomar valores de x suficientemente próximos a a, con x > a , los valores de la imágenes, , están tan próximos a L , como se desee. Se designa por:

Cuando los límites laterales en un punto existen y son iguales, la función tiene límite en ese punto, y viceversa; esto es:

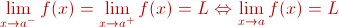Esto es lo que ocurre en el "Ejemplo 1". En cambio, en el "Ejemplo 2", los límites laterales de la función en el punto a no son iguales, por lo tanto, la función no tiene límite en dicho punto:

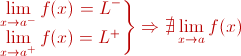2. EJERCICIOS
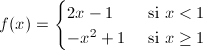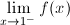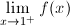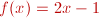Esta unidad interactiva requiere la máquina virtual de Java J2RE.	1.- Dada la función: y apoyándote en la escena, estudiary . SOLUCIÓN: Lo primero que observamos, es que la función , es una función definida a trozos. Es decir, cuando nos aproximamos a a=1 por la izquierda (x<1), . En cambio, cuando nos acercamos por la derecha (x>1), tenemos que . Por tanto: . Luego,

	Mª del Carmen Torres Alonso

	© Ministerio de Educación. Año 2011

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.