
ASÍNTOTAS VERTICALES
 |
LÍMITE
INTINITO EN UN PUNTO ASÍNTOTAS VERTICALES |
| Análisis | |
| 1. LÍMITE
INFINITO EN UN PUNTO |
||
|
Utilizando
el concepto de límite lateral, vamos a ver que se entiende por límite infinito en un punto.
|
||
Ejemplo 1 |
||
|
|
1.- Al
aproximar el punto x a a, ¿qué ocurre con
 y K? y K?2.- ¿Hacia dónde tiende  ? ?
|
|
|
|
3.-
¿Qué
ocurre ahora con  y K, cuando
aproximamos x a a?, y en este caso, ¿hacia
dónde tiende y K, cuando
aproximamos x a a?, y en este caso, ¿hacia
dónde tiende  ? ? |
| Definición de
límite infinito en un punto |
|
|
En respuesta a la segunda
pregunta planteada, decimos que la función
 tiende
a tiende
a  cuando x tiende
a a por
la derecha. En cambio, en el "Ejemplo 2", la función cuando x tiende
a a por
la derecha. En cambio, en el "Ejemplo 2", la función  tiende
a tiende
a  cuando x tiende
a a por la
derecha. cuando x tiende
a a por la
derecha.Más concretamente:
De forma análoga, se pueden
definir los límites laterales infinitos por la izquierda.
Como ejemplo, tenemos que
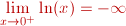 .
Como no tiene límite por la izquierda,
entonces .
Como no tiene límite por la izquierda,
entonces 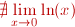 . . |
|
4.- Define en tu cuaderno los límites laterales infinitos por la izquierda de un punto a. |
|
| 2. ASÍNTOTAS
VERTICALES |
|||
|
A
partir de las definiciones de límite lateral por la izquierda y por la
derecha, y limite infinito en un punto, vamos a ver a continuación que
entendemos por una asíntota vertical.
|
|||
Ejemplo 1 |
|||
|
|
1.- ¿Está
definida la función en el punto a=2?
2.- Selecciona el valor del controlador Límites laterales que hace referencia al Límite lateral por la derecha. Si hacemos tender x a a, ¿hacia dónde tiende  ? ?3.- Selecciona ahora el valor del controlador Límites laterales que hace referencia al Límite lateral por la izquierda. En este caso, si hacemos tender x a a, ¿hacia dónde tiende  ? ? |
||
| Ejemplo 2 |
|
|
|
4.-
Responde de nuevo las tres preguntas anteriores aplicadas a este caso.
|
| Ejemplo 3 |
|
|
|
5.-
Responde de nuevo las tres preguntas anteriores aplicadas a este caso.
|
| Ejemplo 4 |
||||
|
|
6.-
Responde de nuevo las tres preguntas anteriores aplicadas a este caso.
|
|||
| Definición de
asíntota vertical |
|
|
Analizados todos los casos,
llegamos a las siguientes conclusiones:
En cualquiera de estas
situaciones, la recta vertical x=a
es una asíntota
vertical de la
función. Además, se dice que la función diverge cuando x toma
valores próximos a a.
|
|
| 3. EJERCICIOS |
|
|
|
1.- Apoyándote
en la escena, calcular los límites de la función
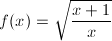 en x=-1 y x=0.
en x=-1 y x=0.SOLUCIÓN:
En primer lugar, es preciso determinar el dominio de la función:  En este caso, tenemos que:
 Esto significa que no existe
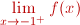 ni ni 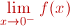 Por tanto:
La función
 tiene
una asíntota vertical en x=0. tiene
una asíntota vertical en x=0. |
2.- Calcula el límite en x=2 de la siguiente función: 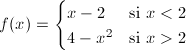 3.- Calcular 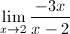 4.- Calcular, si existe, el límite en x=0 de la función: 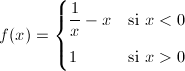 Escribe la ecuación de la asíntota vertical de la función anterior.
5.- Calcula la asíntotas verticales, si las hay de las siguientes funciones: 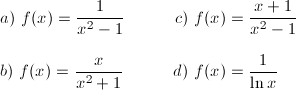 |
|
 |
 |
|||||
| Mª del Carmen Torres Alonso | ||
 |
||
| © Ministerio de Educación. Año 2011 | ||
![]()
Los
contenidos de esta unidad didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.