
 |
LÍMITE DE UNA FUNCIÓN EN UN PUNTO |
| Análisis | |
1. DEFINICIÓN
DE LÍMITE
|
|||
|
|
1.- Si
modificamos el valor de ε. ¿Qué ocurre con el
intervalo que contiene al punto a?.
|
||
|
|
2.-
En este
ejemplo, la función no está definida para a=1. A pesar de que 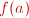 no tiene valor, ¿podemos aproximarnos a L? no tiene valor, ¿podemos aproximarnos a L? |
|
|
3.-
A
diferencia del ejemplo anterior, en este caso tenemos que  , y por tanto la función está definida en este
punto. Si acercamos x a a, ¿hacia dónde se aproxima , y por tanto la función está definida en este
punto. Si acercamos x a a, ¿hacia dónde se aproxima  ? ? |
| Definición de límite de una función en un punto |
|
|
Como habrás podido ver, el
número real L,
es el límite de la función
 ,
en el punto a
puesto que al tomar valores
de x suficientemente
próximos a ,
en el punto a
puesto que al tomar valores
de x suficientemente
próximos aa , sus imágenes,  ,
están tan próximas a L como
se desee. La forma de
expresarlo es la siguiente: ,
están tan próximas a L como
se desee. La forma de
expresarlo es la siguiente: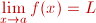 Intuitivamente significa que si
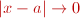 ,
entonces ,
entonces  . .A partir de esta idea intuitiva
de límite se puede formalizar utilizando la definición de entorno que
ya hemos visto.
Decimos que
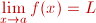 si, para cualquier entorno
de L de
radio ε, por pequeño que este sea, se puede
determinar un entorno de a de
radio δ,
tal que, si x pertenece
al entorno de a
,
entonces si, para cualquier entorno
de L de
radio ε, por pequeño que este sea, se puede
determinar un entorno de a de
radio δ,
tal que, si x pertenece
al entorno de a
,
entonces  pertenece
al entorno de L
. pertenece
al entorno de L
.Esta definición la podemos
escribir de la siguiente forma:
El límite de una función
 cuando x tiende a a es L ,
si para todo números real cuando x tiende a a es L ,
si para todo números real  , existe
otro número real , existe
otro número real  , tal
que, si , tal
que, si  , entonces , entonces 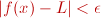 . . Como podéis ver en el ejemplo 2, no
es necesario que a pertenezca
al dominio de
 .
Además, también es posible que .
Además, también es posible que 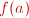 no
coincida con L
,
como ocurre en el ejemplo
3. no
coincida con L
,
como ocurre en el ejemplo
3.No obstante, puede suceder que, al tomar valores de x cada vez más próximos a a, el comportamiento de las imágenes,  ,
sea distinto a ambos lados de a e
incluso que los valores
de las imágenes, ,
sea distinto a ambos lados de a e
incluso que los valores
de las imágenes,  ,
no se aproximen a ningún número. En este último caso, no existe el
límite de la función en dicho punto. ,
no se aproximen a ningún número. En este último caso, no existe el
límite de la función en dicho punto. |
 |
 |
|||||
| Mª del Carmen Torres Alonso | ||
 |
||
| © Ministerio de Educación. Año 2011 | ||
![]()
Los
contenidos de esta unidad didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.