Límites de una función en el infinito. Asíntota Horizontal

Ya hemos visto que ocurre con el límite de una función en un punto, veamos ahora que pasa cuando hacemos tender x hacia

En la siguiente escena tienes representada una función real de variable real. El controlador de nombre Límites en el infinito hace referencia al límite de la función

cuando y cuando . Con el controlador de nombre epsilon puedes modificar el valor de ε.

Selecciona algún valor del controlador Límites en el infinito. Verás que nos aparece en los ejes de coordenadas dos segmentos, uno de color verde de centro L y otro de color rojo que contiene al punto x, el cual se puede desplazar a lo largo de dicho segmento.

Selecciona el valor 1 del controlador de Límites en el infinto, que se corresponde con el límite de la función

cuando .

1.- ¿Qué relación cumple los valores de x y el valor de H?

2.- Si hacemos epsilon pequeño, ¿que le ocurre al valor de H?

3.- Si hacemos tender x hacia

, ¿hacia dónde se aproxima el punto

?

Selecciona ahora el valor 2 del controlador de Límites en el infinto, que se corresponde con el límite de la función

cuando .

4.- Responde de nuevo las tres preguntas anteriores aplicadas a este caso, teniendo en cuenta, que x tiende hacia

Como habrás podido ver, para el primer caso, tenemos que, para cualquier valor que tome ε, se cumple siempre que H < x (para el segundo, se cumple que H > x). Además, por pequeño que sea éste, siempre existe un valor para H, de forma que

está dentro del entorno de centro L y radio ε,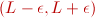

, es decir, cuando x tiende a

(en el otro caso, x tiende a

) tenemos que

se aproxima a L.

Formalmente, lo expresamos de la siguiente forma:

Se dice que el límite de una función, , cuando x tiende a es L si, para cualquier entorno de L de radio ε, por pequeño que sea, se puede determinar un número real, H, a partir del cual las imágenes de x, , pertenecen a dicho entorno de L. Es decir:

Del mismo modo, definimos el límite de

cuando x tiende a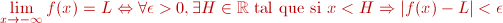

En el caso de que ambos límites coincidan, diremos que límite de

es L cuando x tiende a

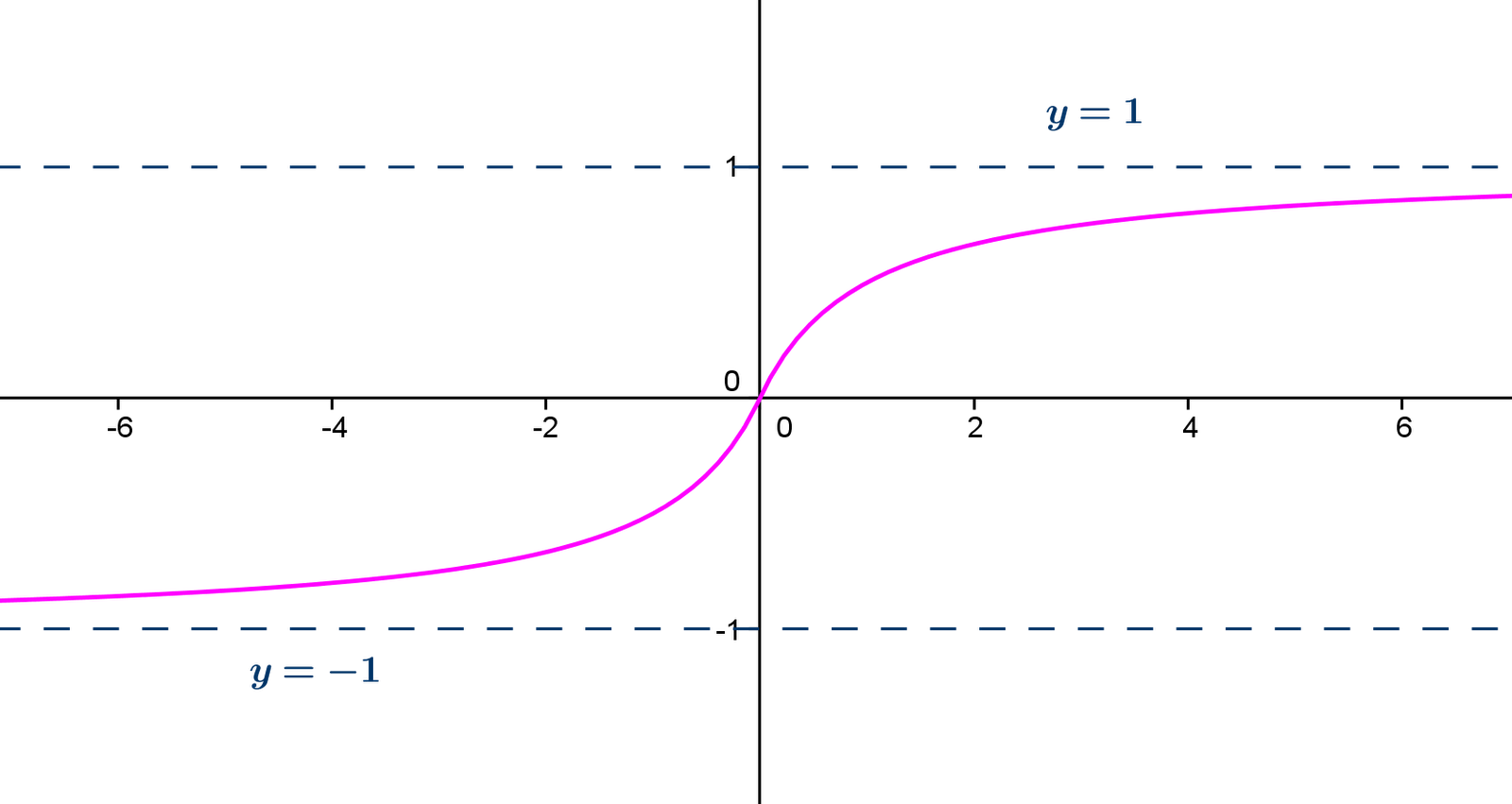
. Es decir:

Realmente, desde un punto de vista geométrico, esto significa que la gráfica de la función tiene puntos tan próximos a la recta y = L (recta horizontal) como queramos para valores suficientemente grandes, en valor absoluto, de la variable x.

A la recta y = L se le llama asíntota horizontal de la función.

En nuestro ejemplo, tenemos que:

Por tanto, la recta y = 3 es una asíntota horizontal de

.

Observa la gráfica de las siguientes funciones:

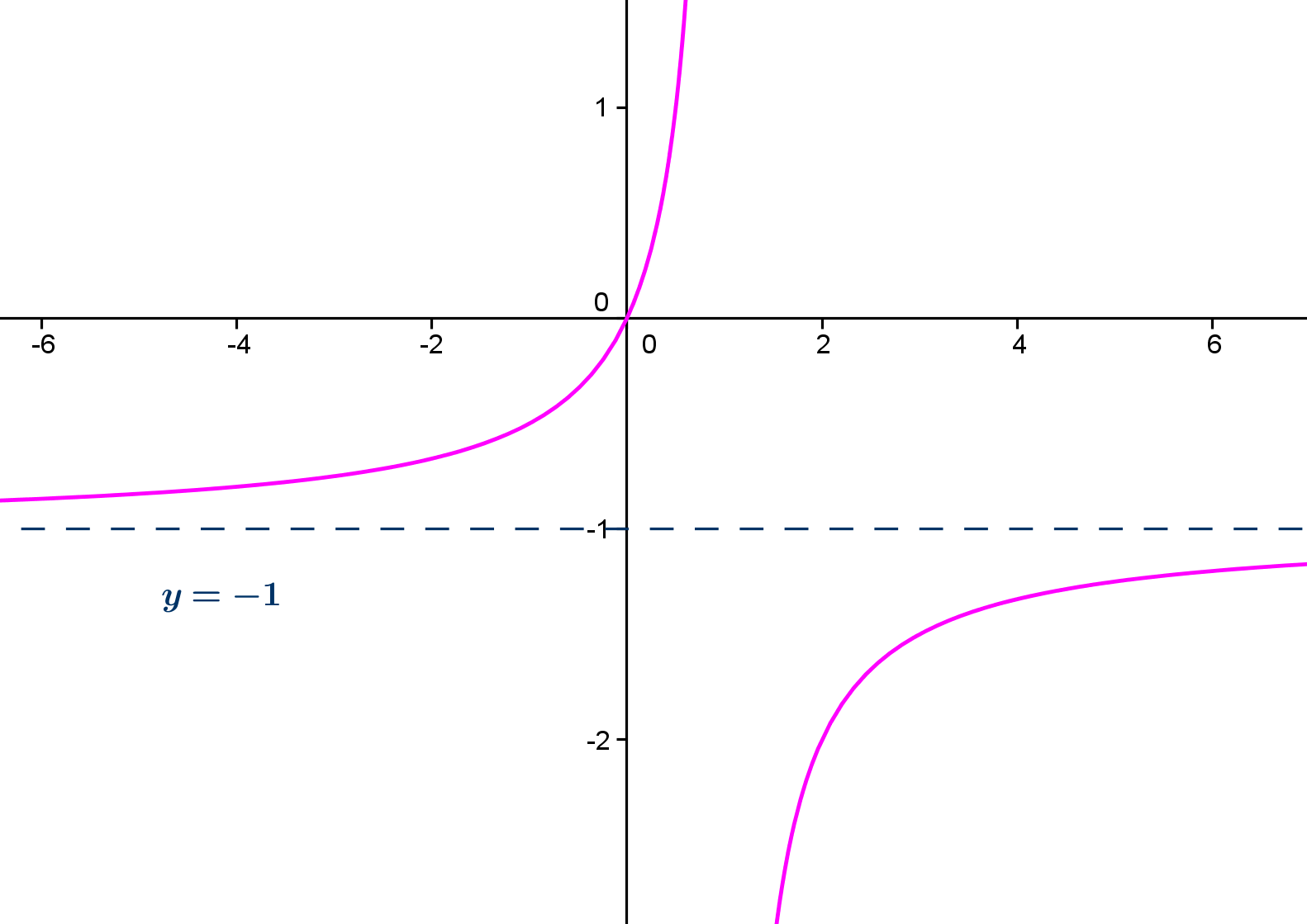
Como puedes ver, una función puede tener asíntotas horizontales distintas cuando (por la derecha) y cuando (por la izquierda) (segunda imagen), o tener solo una de ellas (primera imagen, en este caso la asíntota horizontal es por la derecha).

1.- Ayudándote de la escena, calcula los límites de las siguientes funciones cuando x tiende a infinito.

(para hacerlo en tu cuardeno)

SOLUCION:

1. Si x toma valores muy grandes, los valores de

se a aproximan a 2.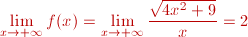

Sin embargo, si x toma valores muy pequeños, los valores de

se a aproximan a -2.

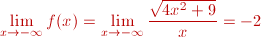Luego,

tiene dos asíntotas horizontales, una en y = 2 por la derecha y otra y = -2 por la izquierda.

En la siguiente escena tienes representadas tres funciones reales de variable real. Basta cambiar el valor del controlador de nombre Funciones para ver cada uno de los ejemplos.

1.- Elige la primera de las funciones que aparecen en la escena y responde a las siguientes preguntas:

Si x toma valores muy grandes, , ¿qué valores toma ?
Si x toma valores muy pequeños, , ¿qué valores toma ?

2.- Haz lo mismo con el resto de ejemplos.

Analizados todos los casos llegamos a las siguientes conclusiones:

Ejemplo 1:

Cuando , tenemos que la función toma valores tan grandes como queramos. Es decir,
Cuando , tenemos que la función toma valores tan grandes como queramos. Es decir,

Ejemplo 2:

Si , la función toma valores tan pequeños como queramos:
Si , la función toma valores tan grandes como queramos: .

Ejemplo 3:

En este caso, aunque $x$ tome valores muy grandes, , o muy pequeños, , la función no se estabiliza alrededor de ningún valor, ni crece ni disminuye indefinidamente. Así pues, diremos que no existe el límite:

Lo anterior lo expresamos de una forma más formal del siguiente modo:

Se dice que el límite de una función

cuando x tiende a

si, para todo número real K, se puede determinar un número real H, a partir del cual las imágenes de x,

, sean mayores que K. Esto es: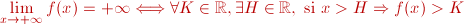

Del mismo modo, podemos definir los otro límites en el infinito como sigue:

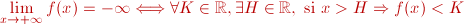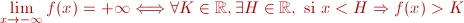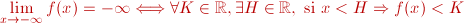1.- Ayudándote de la escena, calcula los límites en el infinito de la función:

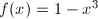SOLUCION:

Cuando x toma valores muy grandes, , la función decrece indefinidamente, y para cualquier número que prefijemos, siempre existirá un valor, a partir del cual,

será menor que ese número:

Cuando x toma valores muy pequeños, , la función crece indefinidamente, y para cualquier número que prefijemos, siempre existirá un valor, a partir del cual,

será mayor que ese número:

	LÍMITES DE UNA FUNCION EN EL INFINITO ASÍNTOTAS HORIZONTALES
	Análisis

3. EJERCICIOS
1.- Determinar la asíntota horizontal de la función: 2.- Determinar las asíntotas horizontales de la función: 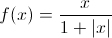3.- Determinar las asíntotas horizontales de la función: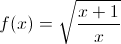

	Mª del Carmen Torres Alonso

	© Ministerio de Educación. Año 2011