There are a sphere, a double cone and a cylinder in the window. They all have the same radius, the perpendicular height of each cone is equal to the radius, and the cylinder height is equal to the diameter. Archimedes discovered that, if we cut them horizontally by a parallel plane, the spherical section  area plus the cone section area is equal to the cylinder section area.

r is the radius of the three figures.
a is the radius of the spherical section.
b is the distance in vertical direction to the centre.
This cone proves that the section radius coincides with the distance to the centre, because the inclination of the slant height is 45º
Sphere section area = π · a²
Cone section area = π · b²
Cylinder section area = π ·  r²
If you add up the first two expressions and apply Pithagoras' theorem to the rectangle triangle of the first figure
π · a² + π · b² = π · (a² + b² ) = π · r²
This also proves that the sphere volume plus the cones volume is equal to the cylinder volume.

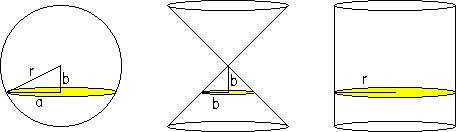With this information, deduce the sphere volume formula.
This property also offers a method to find out the volume of a spherical segment. The spherical segment is the sphere part between two parallel planes. To find out its volume you only have to find out the volume of the corresponding part of the cylinder and to subtract the corresponding part of the cones.

Search for information about Archimedes and write it down in your notebook.