Solids of revolution
First and Second Year of Secondary School
 

A Curiosity.
Correspondence of the spherical surface area and the curved surface area of a cylinder. Spherical zone.

A spherical zone is a spherical surface included between two parallel planes.

 

There are a sphere and a cylinder in the window. Both have the same radius and the cylinder height is the same as the diameter.
Archimedes discovered that, if we cut them horizontally by two parallel planes, the spherical zone area is equal to the corresponding curved surface area of the cylinder.

You can move the planes and check it. In order to do this, click on the up and down triangles or hold them down for a few seconds.

In order to prove it, we are going to look at a very narrow strip.

r is the radius in the two figures.
a is the radius of the spherical zone.
z is the width of the strip of the spherical zone.
c s the width of the strip of the lateral surface of the cylinder, it's the separation between the parallel planes.


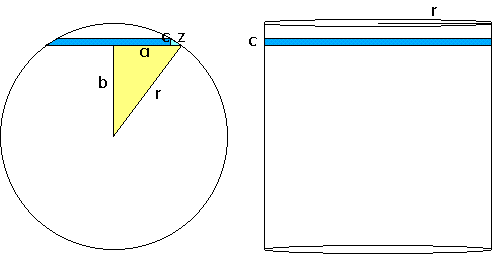The light blue right-angled triangle is similar to the yellow one because their hypotenuse are respectively perpendicular and their edges likewise. Their angles are equal and their sides are proportional.
Consider the ratio hypotenuse /small edge
r/a = z/c
Product of the middle terms = product of the outer terms
a · z = r · c
To find out the surface of a narrow strip, you only have to multiply the circumference by the width.
 The spherical surface area of the strip
= 2 · π · a · z
The cylinder lateral surface area of the strip
= 2 · π · r · c
 With this information, deduce the formula of the spherical zone surface area knowing the sphere radius and  the separation distance of the planes.
       
           
  Eduardo Barbero Corral
 
Spanish Ministry of Education. Year 2007
 
 

Licencia de Creative Commons
Except where otherwise noted, this work is licensed under a Creative Common License