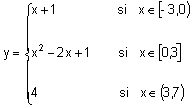FUNCIONES DEFINIDAS MEDIANTE OPERACIONES O 

TRANSFORMACIONES DE OTRAS.

2.1. Funciones definidas a trozos: Ejercicio resuelto 1.

Ahora vamos a estudiar con detenimiento cómo se construye la gráfica de una función definida a trozos.

Sea la siguiente función:

Primer trozo.

En este trozo la expresión analítica es y = x +1, una función lineal, y está definida para los valores de x que son mayores o igual que -3 y menores que 0. Al ser una función lineal con un par de puntos es suficiente para construir la gráfica. Cuando x = -2 => y = -2 +1 = -1; y cuando x = -1 => y = -1 +1 =  0. Es decir la función pasa por los puntos (-2, -1) y (-1, 0).

Ahora en tu cuaderno representa en unos ejes de coordenadas esos dos puntos y dibuja con trazo suave una línea recta que pase por dichos puntos.

Segundo trozo.

En este trozo la fórmula de la función es y = x² - 2x +1, en el intervalo [0, 3] y su representación gráfica es una parábola de eje vertical. Al ser el coeficiente de x² positivo las ramas de la parábola irían hacia arriba. Ahora determinaríamos varios puntos de la parábola y los uniríamos.

Por ejemplo, para x = 0 => y = 0² - 2·0 +1 = 1; para x = 1=> y = 1² - 2·1 +1 = 0; para x = 2  => y = 2² - 2·2 +1 = 1 y para x = 3 => y = 3 ² - 2·3 +1 = 4

Las coordenadas de los puntos serían (0, 1), (1, 0), (2, 1) y (3, 4).

Representa dichos puntos en tu cuaderno y únelos con trazo suave.

Tercer trozo.

En este trozo la función es y = 4 y está definida cuando x pertenece al intervalo (3, 7). La gráfica de la función es una recta horizontal y para dibujarla puedes utilizar los puntos de coordenadas (4, 4) y (5, 4).

Igual que hiciste en el apartado anterior, representa dichos puntos y dibuja con trazo suave la recta que pasa por ellos.

Finalmente dibuja con trazo fuerte cada uno de los trozos de la función.

En esta escena tienes la gráfica de la función que has dibujado en tu cuaderno. Compara ambas gráficas.

Puedes ver los valores de las coordenadas de los distintos puntos de la función arrastrando el control gráfico P.