|
|
|
| Análisis | |
|
|
|
| ÍNDICE | |
Una función
parabólica cualquiera es del tipo f(x)=ax2+bx+c
siendo a,
b, c
números reales con la única restricción de que a
sea distinto de 0
(si fuera a=0, la función ya no sería cuadrática sino afín).
Su representación gráfica
es una parábola.
Su dominio (conjunto de
valores de x que poseen imagen f(x), es decir, valores donde f está
definida) será el conjunto de todos los números reales: Dom(f)=
IR
Su recorrido o rango (conjunto
formado por las imágenes) será Im(f)=I
donde I es un intervalo real que será :
en el caso a>0
y en
el caso a<0:
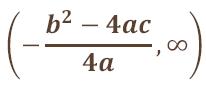
(En el apartado 5 descubrirás el motivo por el cual el recorrido se halla así).
Ejercicio
1 |
Escena
1 |
a) Comprueba cómo son el dominio y el recorrido de las distintas funciones cuadráticas dándoles diferentes valores a los coeficientes a, b y c en la escena 1. b) Halla el dominio y el recorrido de las siguientes funciones y después comprueba con la escena anterior tus soluciones: f(x)=5x2+2x-1 f(x)=-3x2-2x+2 f(x)=-5x2 c)Observa qué tienen en común las gráficas de funciones cuadráticas con a>0 y en qué se distinguen de las que poseen a<0. |
CORTES
CON LOS EJES DE COORDENADAS
Un punto será punto
de corte con el eje OX de la gráfica de f si
es de la forma (p,0) con f(p)=0.
Un punto será punto
de corte con el eje OY de la gráfica de f si
es de la forma
(0,f(0)).
SIMETRÍA
f es
simétrica
respecto del eje:
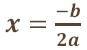
En particular, para el caso b=0, f será simétrica respecto al eje
OY,por lo que en dicho caso, f
será
función par
a) Halla
los puntos de corte con los ejes de coordenadas OX y OY de la
gráfica de f en cada caso: f(x)=2x2-10x+12 f(x)=x2-2x+1 f(x)=x2-2x+6 A la vista de los resultados
reflexiona: ¿es posible que algunas
parábolas no corten al eje OX? ¿Y al eje OY? ¿pueden cortar en más
de un punto a un mismo eje? Comprueba tus resultados y conclusiones
usando la escena 2. b) Comprueba
en la escena 2 qué tipo de simetría tienen y respecto a qué
eje, diferentes gráficas de funciones parabólicas seleccionadas
por tí dando valores a los coeficientes a, b y c. ¿Qué ocurre
si b=0? c) Halla el
eje de simetría e indica el tipo de simetría de cada una de
las funciones siguientes, comprobando con la escena 2 tus soluciones: f(x)=6x2+2x-1;
f(x)=-8x2-3x-2; f(x)=4x2; f(x)=-8x2+7;
f(x)=-8x2+6x d)Observa
qué tienen en común las gráficas de funciones
cuadráticas con a>0 y en qué
se distinguen de las que poseen a<0. La
gráfica de una función parabólica cualquiera
f(x)=ax2+bx+c
: corta
siempre al eje
OY en el punto (0,f(0))=(0,c)
y
corta
al eje OX
en dos puntos (si el discriminante b2-4ac>0),
que son los
puntos
(z,0) y (z',0) * en un punto
(si el discriminante
b2-4ac=0),
que es el punto (-b/(2a),0) y en ningún punto
(si el discriminante
b2-4ac<0). *
z y z' son los valores
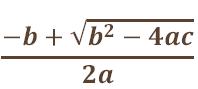y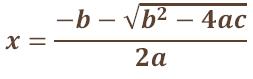
respectivamente.
