COMPOSICIÓN DE MOVIMIENTOS 
Física

Movimiento Parabólico

 

La composición de un movimiento uniforme y otro uniformemente acelerado resulta un movimiento cuya trayectoria es una parábola.

  • Un MRU horizontal de velocidad vx constante.

  • Un MRUA vertical con velocidad inicial voy hacia arriba.

Este movimiento está estudiado desde la antigüedad. Se recoge en los libros más antiguos de balística para aumentar la precisión en el tiro de un proyectil.

Denominamos proyectil a todo cuerpo que una vez lanzado se mueve solo bajo la aceleración de la gravedad.

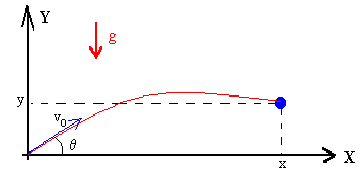
1. Disparo de proyectiles.

Consideremos un cañón que dispara un obús desde el suelo (y0=0) con cierto ángulo θ menor de 90º  con la horizontal.
Las ecuaciones del movimiento, resultado de la composición de un movimiento uniforme a lo largo del eje X, y de un movimiento uniformemente acelerado a lo largo del eje Y, son las siguientes:

Las ecuaciones paramétricas de la trayectoria son

x=v0·cosθ·t
y=v0·senθ·t-gt2/2

Eliminado el tiempo t, obtenemos la ecuación de la trayectoria (ecuación de una parábola)

 

Propuesta de trabajo.

 

Un cañón dispara obuses con una velocidad  inicial de 15 m/s. Calcula el alcance y el tiempo que el obús permanece en el aire para ángulos de 30º, 45º y 60º.

Observa las leyendas en verde de la pizarra y detén el botón del tiempo cuándo la altura sea cero o muy próxima a cero. En este momento la velocidad de llegada y salida coinciden.

Repite la experiencia para una velocidad inicial de 30 m/s.

¿qué conclusiones sacas?

 

1.1. Alcance.

El alcance horizontal de cada uno de los proyectiles se obtiene para y=0.

Su valor máximo se obtiene para un ángulo θ =45º, teniendo el mismo valor para  θ =45+a , que para θ =45-a. Por ejemplo, tienen el mismo alcance los proyectiles disparados con ángulos de tiro de 30º y 60º, ya que sen(2·30)=sen(2·60).

 
1.2. Altura máxima.
La altura máxima que alcanza un proyectil se obtiene con vy=0.

Su valor máximo se obtiene para el ángulo de disparo θ =90º.

 
1.3.Resumen.
Tiempo de vuelo Alcance máximo Altura máxima
Alcance de un proyectil para una velocidad inicial de 60 m/s y diversos ángulos de tiro.
 

Propuesta de trabajo.

 

1.-Se lanza un cuerpo desde el origen con velocidad horizontal de 40 m/s, y con un ángulo  de 60º. Calcular la máxima altura y el alcance horizontal.

2.Un cañón dispara una bala con una velocidad de 46 m/s haciendo un ángulo de 30º por encima de la horizontal. Calcular el alcance, el tiempo de vuelo, y las componentes de la velocidad de la bala. Hallar también la altura máxima.

   
   

 

1.4.Tiro parabólico con altura inicial.      

Se dispara un proyectil desde una altura h sobre un plano horizontal con velocidad inicial v0, haciendo un ángulo θ con la horizontal. Para describir el movimiento establecemos un sistema de referencia como se indica en la figura.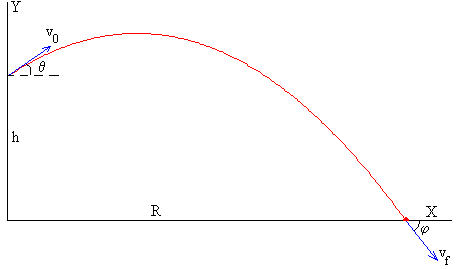

Las componentes de la velocidad del proyectil en función del tiempo son:

vx=v0·cosθ
vy=v0·senθ-g·t

La posición del proyectil en función del tiempo es

x= v0·cosθ·t
y= h+v0·senθ·t-g·t2/2

Estas son las ecuaciones paramétricas de la trayectoria, ya que dado el tiempo t, se obtiene la posición x e y del proyectil.

 

 

Procediendo de igual manera podemos deducir las ecuaciones del alcance máximo, altura máxima y tiempo de vuelo.

                                                                                                                     

3.Un cañón dispara una bala desde lo alto de un acantilado de 200 m de altura con una velocidad de 46 m/s haciendo un ángulo de 30º por encima de la horizontal. Calcular el alcance, el tiempo de vuelo, y las componentes de la velocidad de la bala al nivel del mar. Hallar también la altura máxima. (Hallar primero, las componentes horizontal y vertical de la velocidad inicial

¿QUÉ DIFERENCIAS OBSERVAS?

 
 

 

 

   Luis Ramírez Vicente
Ministerio de Educación, Cultura y Deporte. Año 2006
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.