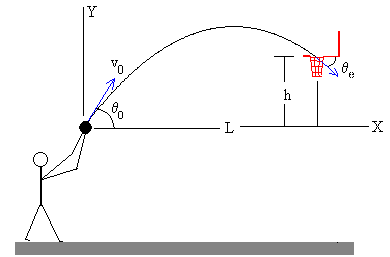
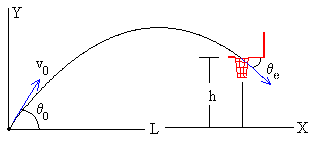
| Establecemos el origen de coordenadas en la posición del
lanzamiento del balón, tal como se muestra en la figura. El
centro del aro está a una altura h y a una distancia L
de la posición inicial del balón. |
 |
|
Consideramos el balón como
una partícula que se lanza desde el origen con una
velocidad inicial v0, haciendo un
ángulo θ0, con la horizontal.
Las ecuaciones del
movimiento, resultado de la composición de un movimiento
uniforme a lo largo del eje X, y de un movimiento
uniformemente acelerado a lo largo del eje Y, son las
siguientes:
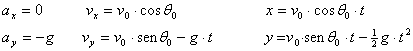
Eliminamos el tiempo t
en las ecuaciones paramétricas de la trayectoria
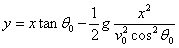 |
|
1.1.Velocidad inicial y ángulo de tiro
Las coordenadas del
punto de impacto son las del centro del aro: x=L,
y=h.
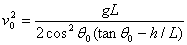
-
Conocida la
velocidad inicial v0, calculamos
los dos ángulos de tiro, resolviendo la ecuación de
segundo grado en tanθ0. Para ello,
utilizamos la relación 1+tan2θ0=1/cos2θ0
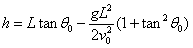
o bien,
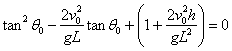
1.2.Ángulo que hace el vector velocidad
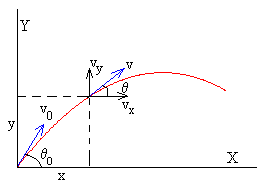 |
El ángulo θ
que hace el vector velocidad v de la
partícula con la horizontal vale
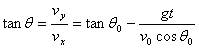
|
como
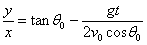
El ángulo θ que
hace el vector velocidad v de la partícula con el
eje X lo expresamos en términos de la posición x
e y de la partícula, en vez del tiempo t.
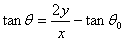 |
|
Para
que el balón entre por el aro, éste debe de estar en la
parte descendente de la trayectoria del balón, tal como
se aprecia en la figura
El
ángulo de entrada θe que forma el
vector velocidad v con la horizontal en el
momento en el que el balón pasa por el centro del aro
x=L, y=h es
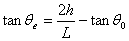
Como θe
es un ángulo negativo (por debajo de la horizontal) su
tangente es negativa, lo que implica que
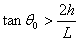
El ángulo de tiro θ0
tiene que cumplir
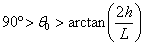
|
|
|



