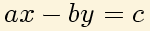
Necesitaremos sustentarnos en un resultado conocido como lema de Bézout o bien:

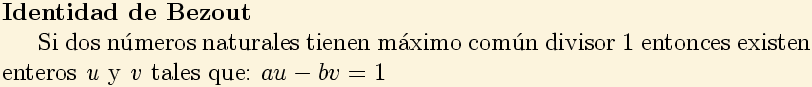
Los números enteros u y v son la solución si c=1.

Fijémonos que la ecuación llamada homogénea tiene soluciones triviales:

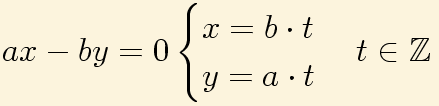
A partir de la solución de Bézout puedo obtener muchas otras sin más que sumarle las de la ecuación homogénea:

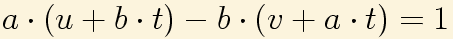
Esta es ya la solución de la ecuación diofántica si c=1, multiplicando por c tenemos la expresión que llamaremos solución general:

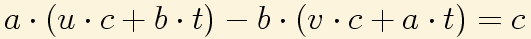
Donde t es un entero cualquiera.

En primer lugar calculemos el máximo común divisor de a=1024 y b=15625 para ver si es 1 y encontremos los números enteros u,v del lema de Bézout.

Usa el botón desplazamiento si los pasos para el cálculo del m.c.d. no caben en la escena anterior.

1.-Encuentra el m.c.d. de 4 y 25 por el método de las divisiones sucesivas. Haz lo mismo para 30 y 7.

2.-Encuentra los números u y v del lema de Bézout para las dos parejas de números anteriores.

4. SOLUCIÓN GENERAL

Formemos ahora la solución general para nuestra ecuación

Ahora tenemos soluciones que dependen del parámetro t, si lo variamos obtenemos otra solución. Pero en el problema del mono y los cocos las soluciones negativas no tienen significado luego hay que descartarlas, tendremos que ir variando el parámetro t hasta encontrar soluciones positivas.

3.-Encuentra soluciones enteras de la ecuación 4x-25y=10. Busca varias soluciones positivas. Haz lo mismo para la ecuación 30x-7y=3.

4.-Piensa como podrías encontrar el número t que diera soluciones positivas en el problema del mono y los cocos.

---

	Antonio Zornoza Manzano
	Ministerio de Educación, Cultura y Deporte. Año 2007

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.