Donde el uno corresponde a cada coco del mono y si restamos los cocos que cada marinero toma quedan los correspondientes en ese reparto a los otros cuatro marineros.

Vamos a sustituir en cascada desde la última a la primera ecuación, para eliminar x₅ de la quinta ecuación necesito que aparezca 4x₅, por lo que multiplico esta ecuación por 4:

Para eliminar ahora x₄ de la cuarta ecuación necesito que aparezca 16x₄, luego multiplico por 16:

Para eliminar ahora x₃ de la tercera ecuación necesito que aparezca 64x₃, luego multiplico por 64:

Hago ahora lo mismo con 256 en la segunda ecuación:

Y por último con 1024 en la primera ecuación:

Obteniendo la ecuación:

En general se llama ecuación diofántica (en honor a Diofanto de Alejandría) a

Donde a y b son naturales y x e y son enteros.

Por tanto tenemos que resolver la ecuación diofántica con a=1024 y b=15625.

1.-Deduce la ecuación diofántica del problema del mono y los cocos para el caso de sólo dos marineros.

2.-Encuentra soluciones para la ecuación que has encontrado.

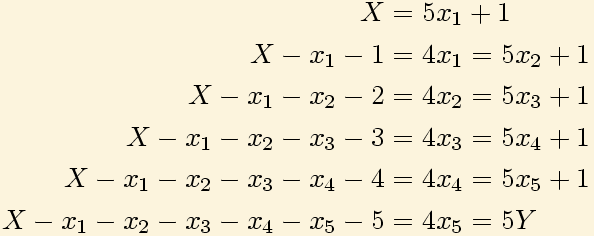
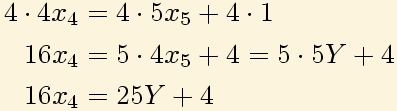
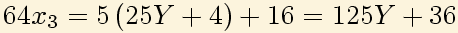
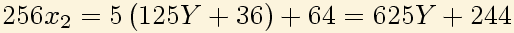
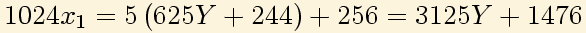
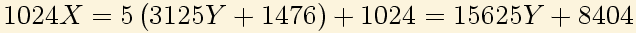
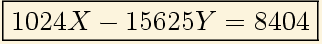
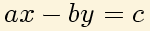
	Antonio Zornoza Manzano
	Ministerio de Educación, Cultura y Deporte. Año 2007

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.