| 4. LA RECTA EN EL PLANO |
Dado en el plano unos ejes
cartesianos de referencia y una recta r, considerando los siguientes elementos:
|
|
1. El segmento a interceptado
por la recta sobre el eje X, se llama abscisa de la recta en el
origen. Análogamente, ordenada de una recta en el origen,
es el segmento b que la recta intercepta sobre el eje Y. El par de números (a,b), con su signo, determinan la recta,
excepto si es a=0 y b=0 (recta que pasa por el origen). 2. El ángulo u que forma la recta con el eje X, se llama
inclinación de la recta. Su tangente se llama pendiente de la recta y se indica
por m. Si m=0, la recta es paralela al eje X. Si m=¥ (=Tg
90o) la recta es paralela al eje Y.
3.Si desde el origen trazamos la perpendicular a la recta dada, se llama ángulo director de la recta al que esta perpendicular forma con el
eje de las X, se indica por w. La distancia del origen a la
recta se indica por d (positivo). El par de números (a,d)
determinan la recta. |
Una pendiente negativa quiere decir que la función es decreciente. Al
desplazarnos hacia la derecha por el eje de abscisas, la recta baja, o dicho de otro modo,
cuando aumenta x, disminuye y.
Una pendiente positiva quiere decir que la función es creciente. Al desplazarnos hacia
la derecha por el eje de abscisas, la recta sube, o dicho de otro modo, cuando aumenta x,
aumenta y. |
| 4.1. ecuación general de la recta |
Se trata de encontrar qué
relación liga a "x" con "y", siendo (x,y)
las coordenadas de los puntos de una recta dada.
|
|
Sea P uno de estos puntos, y N el de intersección de la
recta con el Y (si son paralelas no hay tal N). Trazando por P la perpendicular al eje X,
y por N la paralela, se forma el triángulo rectángulo PNM, cuyos catetos son: Por consiguiente MP = NM tg u, esto es:
De donde, finalmente y = mx + b, donde "m" y "b" son
números cualquiera. Tal es la llamada ecuación explícita de la
recta (función polinómica de primer grado, donde el término independiente es
diferente de cero, denominada función afín.
1. El coste de la energía eléctrica de
una casa viene dada por el precio de la potencia contratada, que es de 12.27 €, y
precio de cada kilovatio por hora es 0.9 €.
a.) ¿Cuál es la función que da la
tarifa conociendo el consumo?
b.) ¿Cuánto ha gastado una familia que
ha consumido 8.25 Kw/h? |
|
- La gráfica de una función afín, y = mx + b , es una recta que no pasa por el origen de coordenadas, sino por el punto
(0,b).
- El coeficiente "m" es aquel que mide la inclinación de la recta
- El termino independiente "b" se llama ordenada en el origen.
Inversamente, los puntos cuyas coordenadas (x,y) satisfacen a una ecuación de la
forma:
o sea, si B ¹ 0, y = -A/B * x - C/B
están situados en una recta cuya pendiente es "m = -B/A" y cuya ordenada en el
origen es "b = -C/B".
|
|
Si en la ecuación (2) falta
"x" por ser (A=0) queda:
By + C = 0 |
o sea |
y = C (cte.) |
Función polinómica de grado cero llamado también función constante, su gráfica es una recta paralela al eje de
abscisas X.
Si falta en dicha ecuación "y" (por ser B = 0), queda:
| Ax + C = 0 |
o sea |
x = K (cte.) |
que representa una paralela al eje Y.
Si falta el término independiente (C = 0), queda:
Ecuación de la recta que pasa por el origen, llamada función lineal. |
Si m > 0, la recta pasa por los cuadrantes I y III.
Si m < 0, la recta pasa por los cuadrantes II y IV.
Más particularidades, se tiene:
| Ecuación del eje X: |
y = 0 |
| Ecuación del eje Y: |
x = 0 |
Por comprender a todos los casos sin excepción se dice que la ecuación (2) es la Ecuación General de la Recta.
|
| 4.2. forma segmentaria de la recta |
Cuando la recta corta a ambos
ejes en puntos distinto del origen su ecuación puede escribirse:
x /a + y/b = 1 |
con: a = -C/A ; b = -C/B |
(3) |
se llama forma segmentaria, porque la
ecuación pone de manifiesto los segmentos a y b. |
| 4.3. ecuación normal de la recta |
|
|
Puesto que:
| a = d / cos a |
| b = d/ sen a |
la recta puede también escribirse:
| x cos a + y sen a -d = 0 |
(4) |
llamada ecuación normal de la recta:
De la ecuación general (2) se pasa a la ecuación normal (4) dividiendo todo los términos por 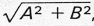 ya que es: ya que es:
|
Para obtener la ecuación normal de una recta
se divide su ecuación general por el módulo del vector (A,B).
|
| 4.4. ecuación vectorial de la recta |
Una recta r
queda determinada vectorialmente dando un punto P
(vector de posición) de la recta y un vector V ,llamado
director, paralelo a dicha recta:
| OX = 0P + t*V (5) |
0
es el origen de coordenadas
X es un punto cualquiera variable de
la recta
0P es el vector posición de un punto P
conocido de la recta
V es un vector dirección conocido,
paralelo a la recta
t es un parámetro. Al dar valores a t,
obtendremos los distintos puntos X de la recta |
|
|
|
Si en la ecuación vectorial se
sustituyen los vectores por sus coordenadas, se obtiene la ecuación
paramétrica de la recta.
| x = Px + t * Vx |
| y = Py + t * Vy |
Para pasar de esta expresión a la ecuación general de la recta (2),
únicamente hay que eliminar el parámetro "t" entre ambas expresiones.
2. Calcula la ecuación de la recta que
pasa por el punto P (2,2) y tiene de vector director V(4,2). Comprueba los resultados con
la escena. Obtén la expresión de la ecuación general.
3. Determina si el punto Q (-5,15),
pertenece a la recta representada. Si no es así determina la recta a la que pertenece con
el mismo vector director. |


