MOVIMIENTOS EN EL PLANO

Movimientos     Traslaciones      Giros      Simetría central

Simetrías

Existen dos tipos de simetría: Simetría central (o simetría respecto a un punto) y Simetría axial (o simetría respecto a un eje).

En el dibujo podemos ver un ejemplo de simetría central, la figura superior (figura 1) se transforma en la figura inferior (figura 2). Se han señalado algunos puntos en la figura superior, figura 1, (A, B, C, D) y los correspondientes en la figura inferior, figura 2, (A', B', C', D'), transformada de la figura 1, mediante una simetría de centro el punto de intersección de las rectas A', B', C y D' .

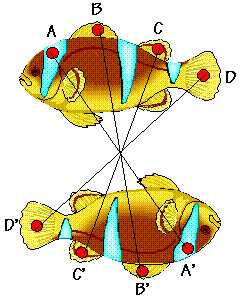
Si te fijas puedes observar que los puntos A', B', C' y D' se obtienen a partir de los A, B, C y D tomando sobre la recta OA, una distancia igual a OA pero en sentido contrario. Esto nos permite obtener el punto A' y de la misma forma se obtienen los puntos B', C' y D'.

En la figura siguiente se muestra un ejemplo de simetría axial. En este caso el eje de simetría es una recta vertical. Las rectas AA', BB', CC' y DD' son ahora perpendiculares al eje de simetría y la distancia desde A al eje coincide con la distancia del punto transformado A' al eje. En definitiva, para obtener el transformado de un punto, en una simetría axial, hay que trazar la perpendicular al eje de simetría que pasa por el punto y situar el punto A', sobre esta perpendicular, a la misma distancia del eje que A.

Movimientos     Traslaciones      Giros      Simetría central

Autor: Belarmino Corte Ramos