4.2 Razones trigonométricas del ángulo diferencia

Si en las fórmulas de la suma cambiamos a por -b y tenemos en cuenta las relaciones entre las razones de ángulos opuestos obtendremos:

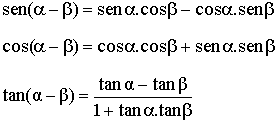
4.3 Razones trigonométricas del ángulo doble

Si en las fórmulas de la suma hacemos a=b obtendremos:

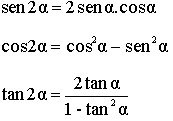
4.4 Razones trigonométricas del ángulo mitad

Si aplicamos la fórmula del coseno del ángulo doble al ángulo a/2 y la formula fundamental de la trigonometría a a/2, obtenemos dos igualdades que al sumarlas nos proporcinan otra igualdad de la que podemos despejar el coseno del ángulo mitad.

Si las restamos obtenemos una igualdad que nos permite obtener la fórmula del seno del ángulo mitad.

Y dividiendo estas últimas obtenemos la fórmula de la tangente del ángulo mitad

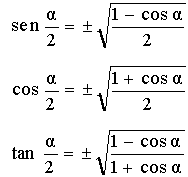
Se utiliza el signo + o el signo - dependiendo del cuadrante en que se encuentre el ángulo a/2 .

4.5 Transformación de sumas y diferencias en productos

En ciertos casos interesa expresar una suma o diferencia como producto. Las fórmulas que lo permiten son:

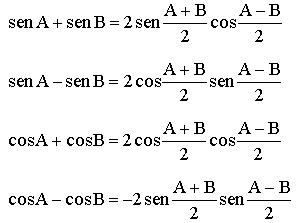
Las primera se obtiene sumando la fórmula del seno de la suma con la del seno de la diferencia y sustituyendo en la igualdad que obtenemos el resultado de resolver el sistema a+b =A, a- b=B.

La segunda restando en lugar de sumar y con el mismo proceso.

La tercera y cuarta se obtienen de forma similar pero utilizando las fórmulas del coseno de la suma y el coseno de la diferencia.

	Ministerio de Educación, Cultura y Deporte. Año 2000