
|
LÍMITE Y CONTINUIDAD DE FUNCIONES
|
Volver
al índice
1.3.- Cálculo del dominio de funciones racionales
Para el cálculo del DOMINIO de las funciones con la x en el
denominador o racionales, hay que tener en cuenta que el denominador de una fracción
nunca puede ser nulo.
Luego los valores de x que hagan cero el denominador de la función no pueden
pertenecer al DOMINIO de la misma.
A) En esta escena se representan las funciones
racionales del tipo  (en verde), y la recta del denominador y=cx+d (en rojo obscuro). Podemos cambiar los valores de a, b, c y d para
obtener distintas funciones del mismo tipo. También tenemos un punto P de la función racional, podemos ver en la escena sus
coordenadas, y cambiar la abcisa del punto, x, en el botón inferior.
(en verde), y la recta del denominador y=cx+d (en rojo obscuro). Podemos cambiar los valores de a, b, c y d para
obtener distintas funciones del mismo tipo. También tenemos un punto P de la función racional, podemos ver en la escena sus
coordenadas, y cambiar la abcisa del punto, x, en el botón inferior.
Para averiguar qué punto no pertenece a la función se hace el denominador cx+d=0
De donde x=-d/c . Vemos que es el punto donde la recta del denominador corta al
eje X.
Es el punto señalado en rojo en la escena, y el que no pertenece al DOMINIO de la
función racional.
|
|
Así en el inicio de la escena está representada la
función
donde el denominador es cero para x = -3
Por tanto el DOMINIO de esta función es
Todos los números reales quitando -3.
Prueba a introducir en la escena el valor de x=-3
y observa lo que ocurre. |
EJERCICIO 5
Halla el DOMINIO de las siguientes funciones, comprobando
tus resultados en la escena anterior:
a) 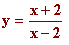 b)
b) 
B) Si el denominador de la fracción es de
segundo grado, puede haber hasta dos puntos que anulen el denominador. En dichos puntos no
existirá la función, y el DOMINIO serán todos los números reales quitando los valores
de x que hacen cero el denominador.
Por tanto lo primero que hay que hacer para hallar el DOMINIO es igualar a cero el
denominador y resolver la ecuación resultante.
Veámoslo gráficamente:
En esta escena tenemos representadas funciones racionales (en
verde) cuyo denominador es un polinomio de segundo grado ax2+bx+c (en rojo obscuro).
Los coeficientes a, b y c podemos cambiarlos con los botones inferiores y así obtener
distintas funciones.
|
|
Los puntos marcados en rojo son los que
hacen cero el polinomio del denominador, y por tanto donde no existe la función racional.
También podemos ver un punto P de la función racional y
sus coordenadas.
Prueba a dar los valores que anulan el denominador a la abcisa del punto P, x, en la parte inferior de la escena, y observa lo que ocurre. |
En el inicio de la escena aparece la función 
Si se iguala a cero el denominador x2-4x+3=0, obtenemos dos soluciones: x=1,
x=3, donde corta la parábola al eje X.
Podemos ver en la escena que justamente en esos puntos es donde no existe la función
racional.
Por tanto el |
DOMINIO de la función  |
es |
D=R-{1,3} |
Nota: La expresión entre llaves {1,3} sólo incluye a los valores de x aislados,
1 y 3. No confundir con [1,3] que indica el intervalo cerrado [1,3], o sea todos los
valores de x entre 1 y 3, incluidos 1 y 3. Si escribimos (1,3) sería también un
intervalo, pero abierto, serían todos los valores de x entre 1 y 3, pero no están
incluidos ni el 1 ni el 3.
EJERCICIO 6
Halla el DOMINIO de las siguientes funciones, comprobando
tus resultados en la escena anterior:
1.4.- Cálculo del dominio de funciones con raíces en el denominador
A) En esta escena tenemos representadas
funciones del tipo  , junto con la función que aparece dentro de la raíz del denominador,
o sea la función y=ax+b (en rojo obscuro).
, junto con la función que aparece dentro de la raíz del denominador,
o sea la función y=ax+b (en rojo obscuro).
Cuando esta función polinómica es negativa, no existe la
raíz, tampoco el denominador y tampoco la función 
Cuando la función polinómica es cero, existe la raíz,
que será cero, pero al ser cero el denominador, no existe la función 
|
|
Hemos señalado en rojo el punto que hace
cero el denominador, donde la recta y =ax+b corta al eje X, y sombreado en gris la parte
negativa de dicha recta. Por tanto en el punto rojo y en el intervalo
sombreado no existe la función 
como puede verse en la escena.
Dando a la abcisa del punto P, x, un valor dentro del DOMINIO, podemos ver también la
ordenada del punto. Observa qué ocurre cuando le das a x un valor fuera del DOMINIO de la
función. |
Para hallar analíticamente el DOMINIO de la función  , hay que averiguar
cuándo la función polinómica y=ax+b es positiva, esto es resolver la inecuación
ax+b>0 (Puedes recordar como se hace en el punto 1.1.2
de esta lección)
, hay que averiguar
cuándo la función polinómica y=ax+b es positiva, esto es resolver la inecuación
ax+b>0 (Puedes recordar como se hace en el punto 1.1.2
de esta lección)
En el inicio de la escena la función que aparece es 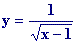 , para hallar su
DOMINIO analíticamente hacemos x-1>0, de donde x>1. DOMINIO = (1,¥)
, para hallar su
DOMINIO analíticamente hacemos x-1>0, de donde x>1. DOMINIO = (1,¥)
(Ahora ponemos paréntesis en el intervalo, pues en x=1 no existe la función, si nó
sería cero el denominador)
Para hallar el DOMINIO gráficamente basta representar la función polinómica y=ax+b
y ver el intervalo donde esta función es positiva, pues ese intervalo será el DOMINIO
de la función 
En el caso de la función 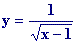 , basta mirar en el inicio de la escena que el intervalo donde
y=x-1 es positiva es a la derecha de x=1. Por tanto el DOMINO es (1,¥)
, basta mirar en el inicio de la escena que el intervalo donde
y=x-1 es positiva es a la derecha de x=1. Por tanto el DOMINO es (1,¥)
EJERCICIO 7
Halla el DOMINIO de las siguientes funciones, comprobando
tus resultados en la escena anterior:
a) 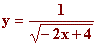 |
b)  |
B) En esta escena tenemos representadas
funciones del tipo 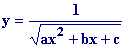 , junto con la función que aparece dentro de la raíz del denominador, o
sea la función y=ax2+bx+c
, junto con la función que aparece dentro de la raíz del denominador, o
sea la función y=ax2+bx+c
Cuando esta función polinómica es negativa, no existe la
raíz, tampoco el denominador y tampoco la función 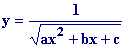
Cuando la función polinómica es cero, existe la raíz,
que será cero, pero al ser cero el denominador, no existe la función 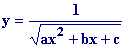
El punto P, es una punto de la función, del cual
puedes ver sus coordenadas, y que puedes mover cambiando su valor de x.
|
|
Hemos señalado en rojo los puntos que
hacen cero el denominador, y sombreado en gris la parte negativa de la función y=ax2+bx+c
Por tanto en los dos puntos rojos y en el intervalo sombreado no existe la
función 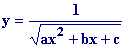
como puede verse en la escena.
Observa lo que ocurre cuando le das a x un valor fuera de su DOMINIO. |
Por tanto para hallar analíticamente el DOMINIO de la función 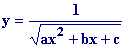 hay que estudiar
el signo de la función polinómica y=ax2+bx+c (Puedes recordar como se
hace en el punto 1.2
de esta lección)
hay que estudiar
el signo de la función polinómica y=ax2+bx+c (Puedes recordar como se
hace en el punto 1.2
de esta lección)
Para hacerlo gráficamente basta representar la función polinómica y=ax2+bx+c
y ver los intervalos donde esta función es positiva, pues esos intervalos serán el
DOMINIO de la función 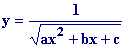
En el inicio de la escena podemos ver que el DOMINIO de la función 
es (-¥,1) U (3,¥)
EJERCICIO 8
Halla el DOMINIO de las siguientes funciones, comprobando
tus resultados en la escena anterior:
CONCLUSIONES
RAZONES POR LAS QUE EL DOMINIO DE DEFINICIÓN DE
UNA FUNCIÓN PUEDE RESTRINGIRSE |
EJEMPLOS |
 Imposibilidad de realizar alguna operación con ciertos valores
de x: Imposibilidad de realizar alguna operación con ciertos valores
de x:
|
 Contexto
real del que se ha extraído la función Contexto
real del que se ha extraído la función |
V=a3 es el volumen de un cubo de arista a. La
función no está definida para a nulo o negativo: D=(0,¥) |
 Por
voluntad de quien propone la función Por
voluntad de quien propone la función |
y=2x+5; xÎ[1,4]
D=[1,4] porque así lo deseamos |
 Funciones
a trozos Funciones
a trozos |
 no está definida para x=2 no está definida para x=2
D=R-{2} |
 Por la naturaleza de la función: Por la naturaleza de la función:
 Funciones
trigonométricas Funciones
trigonométricas |
y=tag(x) no está definida en x=p/2+2kp
D=R-{p/2+2kp} |
 Funciones
logarítmicas Funciones
logarítmicas |
y=ln(x) no está definida para x=0 ni para x<0
D=(0,¥) |
|
Volver
al índice
Autora: Ángela Núñez Castaín
 |
|
|
Ministerio de Educación, Cultura y Deporte. Año 2000 |
|
| |
