|
LÍMITE Y CONTINUIDAD DE FUNCIONES
|
Volver al índice
1.- DOMINIO DE
DEFINICIÓN DE UNA FUNCIÓN
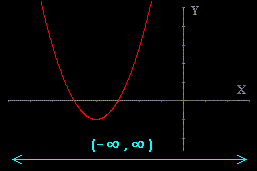
En esta escena están representadas dos funciones: f1: y = x2 +
8x + 15 y f2: y =
También puedes ver un punto P de la función polinómica f1 y un punto Q de la radical
f2, con sus respectivas coordenadas.
Con los botones inferiores puedes cambiar las abcisas de ambos puntos, viendo como cada
punto recorre su gráfica.
|
|
EJERCICIO 1
Escribe en tu cuaderno las respuestas a las siguientes preguntas,
razonándolas con la ayuda de la escena: a)
¿Existe la función
y = x2 + 8x + 15 para cualquier valor de x?
b) ¿Qué ocurre cuando le das a x (Q.x) un valor negativo en
la función 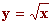 ?
¿Existe esta función para cualquier valor de x? ?
¿Existe esta función para cualquier valor de x?
|
Habrás podido deducir del ejercicio anterior que la función polinómica
y = x2 + 8x + 15 existe para cualquier valor de x, o sea podemos dar a x
un valor cualquiera y siempre se obtendrá un valor real de y. Decimos que esta función
está definida en todo R (números reales) o bien su dominio
de definición es R o (-¥,¥).
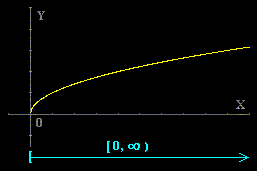
Sin embargo la función y =  no existe cuando x es negativo, no podemos dar a x
valores negativos. Su dominio de definición es [0,¥).
no existe cuando x es negativo, no podemos dar a x
valores negativos. Su dominio de definición es [0,¥).
| Dominio de f |
Þ |
Df |
= |
conjunto de valores de x |
tales que |
f(x) existe o es un número real |
PRIMERA CONCLUSIÓN
Las funciones polinómicas tienen D=R
Las funciones con raíces cuadradas, o de índice par, no existen cuando el radicando es negativo.
Volver al índice
1.1.- Cálculo del dominio de funciones radicales de un polinomio de primer
grado
El DOMINIO de las funciones 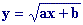 serán los valores de x para los cuales ax+b³0 serán los valores de x para los cuales ax+b³0 |
1.1.1.- Gráficamente
En esta escena está representada la función 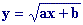 , y la función que aparece en el
radicando, o sea debajo de la raíz, y = ax +b
, y la función que aparece en el
radicando, o sea debajo de la raíz, y = ax +b
| ax+b³0 |
y=ax+b positiva |
Þ |
gráfica de y=ax+b encima eje X |
Þ |
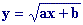 EXISTE EXISTE |
| ax+b nº positivo |
Þ |
 es nº
real es nº
real |
| ax+b<0 |
y=ax+b negativa |
Þ |
gráfica de y=ax+b debajo eje X |
Þ |
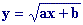 NO EXISTE NO EXISTE |
| ax+b nº negativo |
Þ |
 no es nº
real no es nº
real |
Y si das los valores a=-3 y b=5, verás que el DOMINIO de
la función 
es D = (-¥, 5/3]
Volver al índice
1.1.2.- Analíticamente
Analíticamente para hallar el DOMINIO de la función 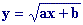 , se resuelve la
inecuación ax+b³0, de donde se deduce el DOMINIO. , se resuelve la
inecuación ax+b³0, de donde se deduce el DOMINIO. |
Por ejemplo para hallar el DOMINIO de la función 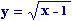 se procede así:
se procede así:
x-1 ³ 0 Þ x ³ 1 Þ a partir 1
hacia la derecha Þ D = [1, ¥)
Y para hallar el DOMINIO de la función  así:
así:
-3x + 5 ³ 0 Þ -3x ³ -5 Þ 3x £ 5 Þ x £ 5/3 Þ a
partir de 5/3 hacia la izquierda Þ D = (-¥, 5/3]
EJERCICIO 2
Calcula analíticamente en tu cuaderno el DOMINIO de las
siguientes funciones, comprobando tus resultados en la escena anterior:
a)  b)
b) 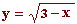
Volver al índice
1.2.- Cálculo del dominio de funciones radicales de un polinomio de segundo
grado
El DOMINIO de las funciones 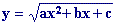 serán los valores de x para los
cuales ax2+bx+c³0 serán los valores de x para los
cuales ax2+bx+c³0 |
1.2.1.- Gráficamente
En esta escena está representada la función 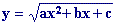 , y la función que aparece en el
radicando, o sea debajo de la raíz, y = ax2 +bx+c
, y la función que aparece en el
radicando, o sea debajo de la raíz, y = ax2 +bx+c
| ax2+bx+c³0 |
y=ax2+bx+c positiva |
Þ |
gráfica de y=ax2+bx+c encima
eje X |
Þ |
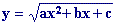 EXISTE EXISTE |
ax2+bx+c
nº positivo |
Þ |
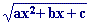
es nº real |
| ax2+bx+c<0 |
y=ax2+bx+c negativa |
Þ |
gráfica de y=ax2+bx+c debajo
eje X |
Þ |
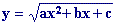
NO EXISTE |
ax2+bx+c
nº negativo |
Þ |
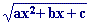
no es nº real |
EJERCICIO 3
Calcula en tu cuaderno el DOMINIO de las siguientes funciones,
representando previamente las funciones que aparecen debajo de la raíz, y comprobando tus
resultados en la escena anterior:
a)  b)
b)  c)
c) 
d)  e)
e) 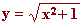 f)
f) 
Volver al índice
1.2.2.- Analíticamente
Analíticamente para hallar el DOMINIO de la función 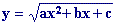 , se resuelve la
inecuación ax2 +bx+c³0, de donde se deduce el
DOMINIO. , se resuelve la
inecuación ax2 +bx+c³0, de donde se deduce el
DOMINIO. |
RESOLUCIÓN DE LA INECUACIÓN
ax2 +bx+c³0
Primero hay que factorizar la función polinómica y=ax2+bx+c
Para ello se resuelve la ecuación ax2 +bx+c = 0 y se pueden dar tres casos:
A) La ecuación tiene dos soluciones reales distintas x1 y x2 ,
por tanto se anula en dos puntos, en los cuales la función cambia de signo.
La factorización será: y=ax2+bx+c = a (x-x1)(x-x2)
Se divide la recta real en tres intervalos (-¥,x1);
(x1,x2); (x2,¥)
suponiendo x1< x2
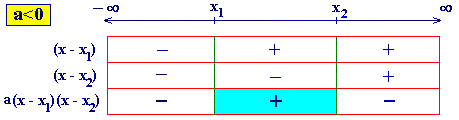
Y se estudia el signo del producto a (x-x1)(x-x2)
a través del de sus factores: 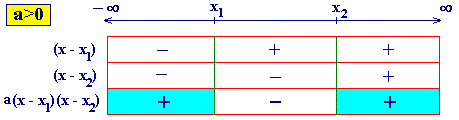
| Solución de la inecuación ax2 +bx+c³0 |
(-¥, x1] U
[x2, ¥) |
DOMINIO de la función 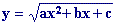 |
(-¥, x1] U
[x2, ¥) |
| Solución de la inecuación ax2 +bx+c³0 |
[ x1, x2 ] |
DOMINIO de la función 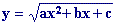 |
[ x1, x2 ] |
B)
La ecuación tiene una solución
real doble x1 , por tanto se anula en un sólo punto, y en los demás la
función tiene siempre el mismo signo.
La factorización será: y=ax2+bx+c = a (x-x1)2
En este caso (x-x1)2 ³0 siempre
a>0 |
a(x-x1)2³0 |
Solución inecuación ax2+bx+c³0 |
R todos los nos reales |
DOMINIO de la función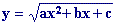 |
D=R |
a<0 |
a(x-x1)2£0 |
x = x1
|
D=x1 |
C) La ecuación no tiene
solución real
y=ax2+bx+c no se factoriza, no se anula en
ningún punto, y la función siempre tiene el mismo signo.
| a>0 |
ax2+bx+c>0 |
Sol.inecuación ax2+bx+c³0 |
R todos los nos reales |
DOMINIO de la función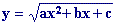 |
D=R |
| a<0 |
ax2+bx+c<0 |
No hay solución
real |
No existe la función |
, pues al final no
son tres casos, sino seis, pues de cada apartado
hemos sacado dos.
La mejor forma de tener claro el cálculo del DOMINIO de las funciones 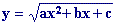
es hacer el estudio analítico y a continuación el gráfico, para entender mejor cada
caso.
Resuelve detenidamente el ejercicio siguiente y te aseguro
EJERCICIO 4
Dadas las funciones:
a)  b)
b)  c)
c) 
d)  e)
e) 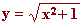 f)
f) 
Primero) Coges la primera y hallas
su DOMINIO analíticamente según las instrucciones dadas en el apartado 1.2.2
de esta unidad y que está más arriba en esta misma página.
Segundo) Introduces los valores de
a, b y c en la escena de más arriba y que pertenece al apartado 1.2.1
de esta misma página, para ver su DOMINIO gráficamente.
Tercero) Repite los aparatados
anteriores para las demás funciones.
Las seis funciones dadas corresponden a los seis casos posibles
que se pueden dar, pero no están en el mismo orden.
Volver al índice
Autora: Ángela Núñez Castaín
 |
|
|
Ministerio de Educación, Cultura y Deporte. Año 2000 |
|
| |