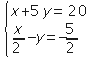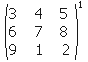| MONOGRÁFICO: Matemáticas y las TIC |
 |
 |
 |
| EQUIPAMIENTO TECNOLÓGICO - Didáctica de la tecnología | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Escrito por Elvira Mifsud | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Lunes, 28 de Junio de 2010 00:00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Existe una gran variedad de aplicaciones dentro del Software Libre, dedicadas a facilitar al profesor de matemáticas la introducción de las tecnologías de la información y comunicación en su tarea docente. Algunas de ellas son sumamente amplias y completas, pero también complejas. Estas aplicaciones se pueden utilizar en la secundaria obligatoria y abarcan en gran medida el currículo. Por otra parte y al ser tan sencillas, el mismo alumno puede instalarlas para trabajar desde su casa y realizar sus ejercicios y construcciones.
DMATHSIntroducciónSi necesitamos insertar fórmulas en nuestros documentos, o en nuestro caso, en los ejercicios o exámenes de matemáticas, OpenOffice.org pone a nuestra disposición una extensión llamada dmaths. Cualquier tarea que requiera la utilización de fórmulas, gráficas o diagramas en materias como matemáticas, estadística o física puede utilizar esta aplicación, que se integra en el procesador de textos OpenOffice.org Writer como una barra de herramientas. Es por tanto, una solución práctica en relación a la creación/edición de fórmulas matemáticas. En este artículo vamos a mostrar cómo utilizar esta aplicación, como complemento a las herramientas matemáticas que estamos estudiado. Características y requisitosDmaths tiene licencia GNU/GPL y está disponible para Windows, GNU/Linux y Mac OS. La página del proyecto es http://www.dmaths.org/.
El único requisito que tiene es disponer de una instalación previa del paquete de oficina OpenOffice.org, ya que se integra en él. InstalaciónEn primer lugar descargamos el paquete comprimido Dmaths32.zip de la página web http://extensions.services.openoffice.org/en/download/1734
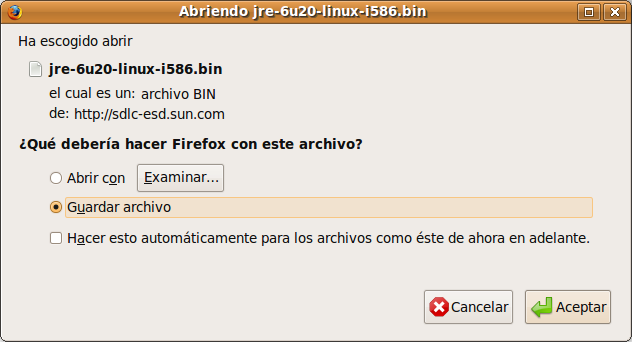
El archivo zip contiene, además de la extensión de OpenOffice.org correspondiente (.oxt) un conjunto de archivos complementarios con información sobre la instalación, licencia, novedades de cada nueva versión, notaciones matemáticas y unos resúmenes de uso muy interesantes. Para realizar la instalación abrir el archivo install.odt y pulsar en el botón correspondiente a la instalación en el idioma que se quiera. No está disponible todavía en español. Para que se puedan ejecutar la macros incluidas en este archivo hay que habilitar un modo de seguridad de ejecución de macros desde OpenOffice.org. Para ello ir a Herramientas > Opciones > Seguridad y en Seguridad de macros habilitar el nivel medio. Al pulsar en el botón correspondiente a la instalación se muestra un mensaje de petición de confirmación de ejecución de macros, mostrando el mensaje:
El proceso de instalación es diferente en función de los permisos del usuario que ejecuta la acción. Si se trata de un usuario 'normal' la instalación se hará para su uso particular (monousuario). Si se trata de un usuario administrador la instalación se hará para todos los usuarios. Lo que tiene que quedar claro es que no se debe intentar descomprimir el archivo DmathsAddon.oxt. A continuación muestra los términos de la licencia, que para poder Aceptar hay que listar hasta el final del texto mostrado. Finaliza la instalación y se muestra:
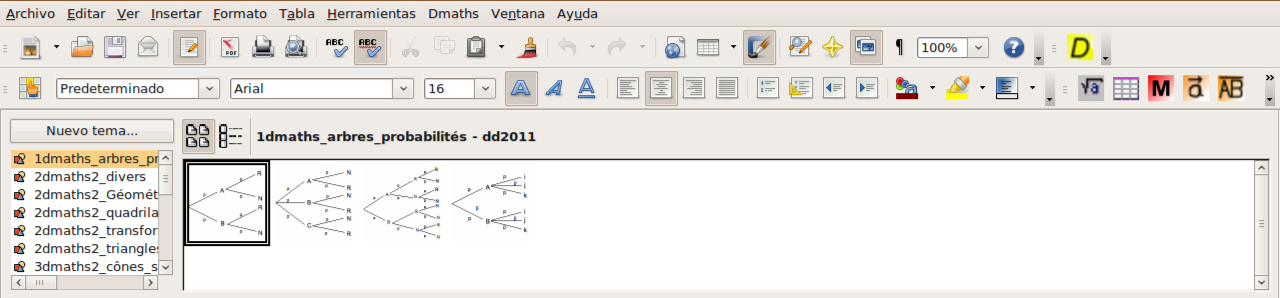
La figura siguiente muestra el aspecto del Writer con Dmaths incluida:
Desde este archivo también podemos actualizar la extensión o desinstalarla. Esta opción también está disponible dentro del nuevo menú creado (Dmaths > Remove/Update Dmaths). Es MUY IMPORTANTE tener en cuenta que si un usuario, que se ha instalado dmaths para su uso particular, elimina dmaths y lo intenta volver a instalar, aunque diga que se ha instalado correctamente, no lo ha hecho. En este caso, como la instalación de dmaths es por usuario, hay que eliminar el archivo .openoffice.org o moverlo a otro directorio y volver a realizar la instalación de dmaths. Pero hay que tener en cuenta que si se han realizado otras tareas de personalización del OpenOffice.org se perderán. ConfiguraciónLas opciones del menú de dmaths son las siguientes:
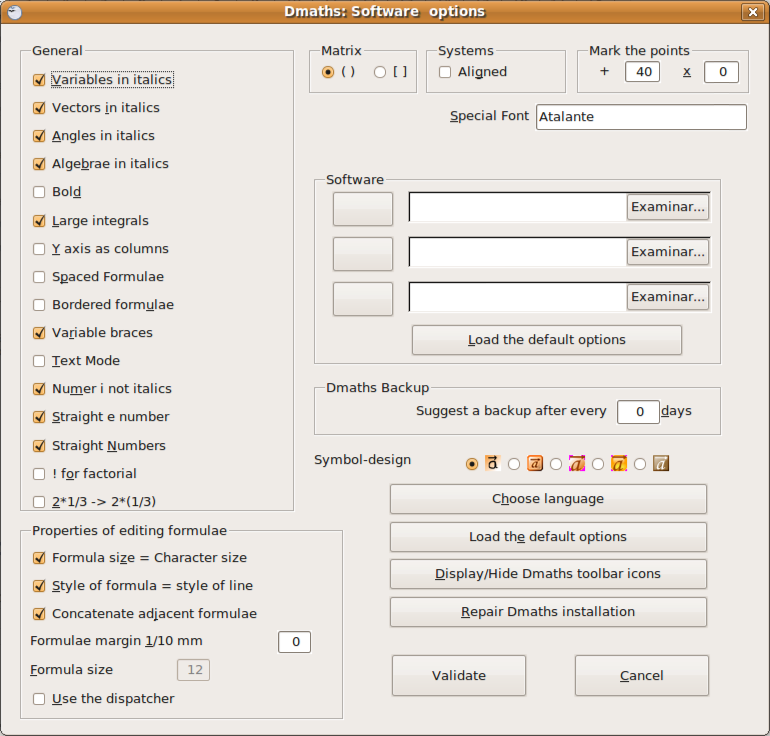
En la barra se incluyen opciones para crear rejillas, crear sistemas de ecuaciones, estudiar el crecimiento y decrecimiento de funciones, dibujar curvas, crear fórmulas de tipo fracción, raíz, límites, etcétera. De estas opciones vamos a entrar en la de configuración: Select Dmaths options identificada por la O amarilla. Hay que tener en cuenta que algunas opciones obligan a reiniciar el OpenOffice para que surtan efecto. En cuyo caso primero se deberá guardar el documento y que se recuperará automáticamente al reiniciar.
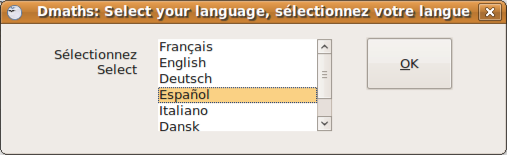
De toda esta gran cantidad de opciones de configuración sólo vamos a cambiar el idioma a Español. Para ello pulsamos en Choose Language y seleccionamos el Español.
Nos indica que se ha realizado el cambio de idioma a castellano, pero que afecta a ciertas opciones de configuración cuyo texto explicativo aparecerá ya en castellano.  Además de la barra de herramientas incluida con Dmaths, la Galería (Herramientas > Galería) se ha rellenado con una gran cantidad de temas específicos de matemáticas, como muestra la figura siguiente:
Si necesitamos ocultar temporalmente la barra de herramientas incluida por Dmath hay que ir a Ver > Barra de Herramientas y deseleccionar la barra Dmaths-Addon, o pulsando sobre el icono con una 'D' en la opción Cerrar barra de herramientas. Las macrosHemos visto que las opciones de trabajo de dmaths vienen con diferentes colores. Tiene su significado.
Utilización de DmathsUna vez tenemos Dmaths instalado nos planteamos la pregunta ¿y qué podemos hacer con Dmaths? ¿en qué nos puede ayudar? Vamos a mostrar algunos ejemplos muy sencillos de utilización de la herramienta como iniciación. En base a ellos el profesor puede experimentar y ahondar en sus funcionalidades. Escribir una expresión algebraica
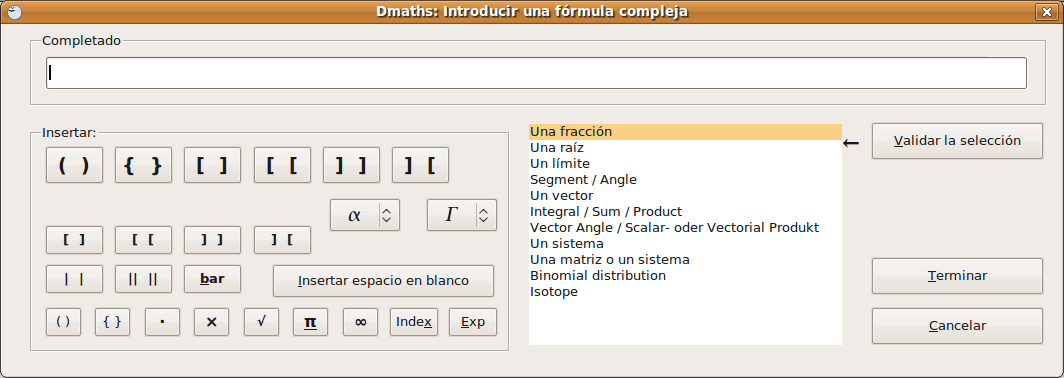 Vamos a escribir una fracción: seleccionamos la opción Una fracción y pulsamos en Validar la selección. 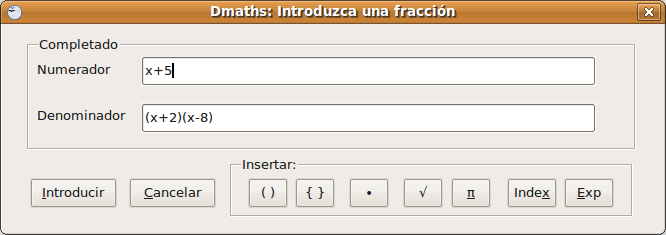 Nos muestra: Pulsamos en Introducir y vuelve a la ventana anterior para seguir escribiendo la expresión algebraica o en nuestro caso para Terminar. 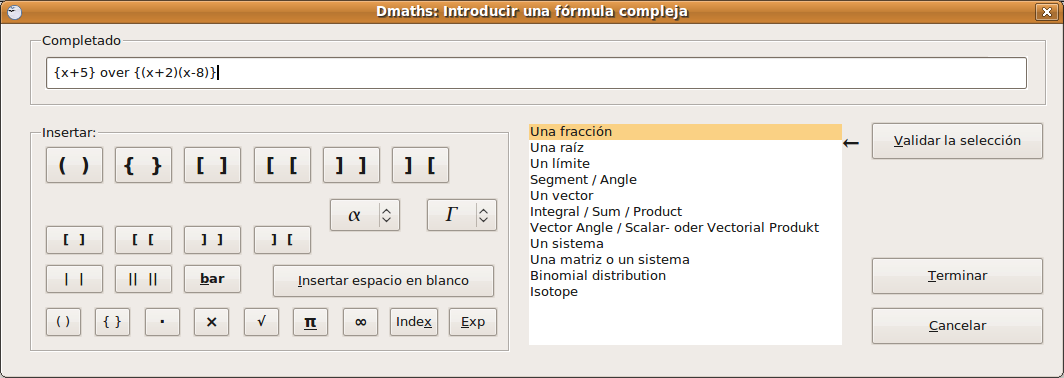 La fórmula obtenida, que en nuestro caso una sencilla expresión algebraica es a siguiente:
Escribir una función
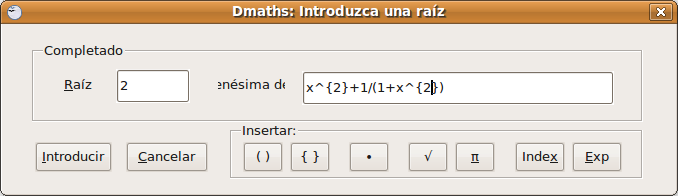 Cuando pulsamos Introducir vuelve a la ventana de fórmula en la que aparece ya la función formada hasta ese momento. 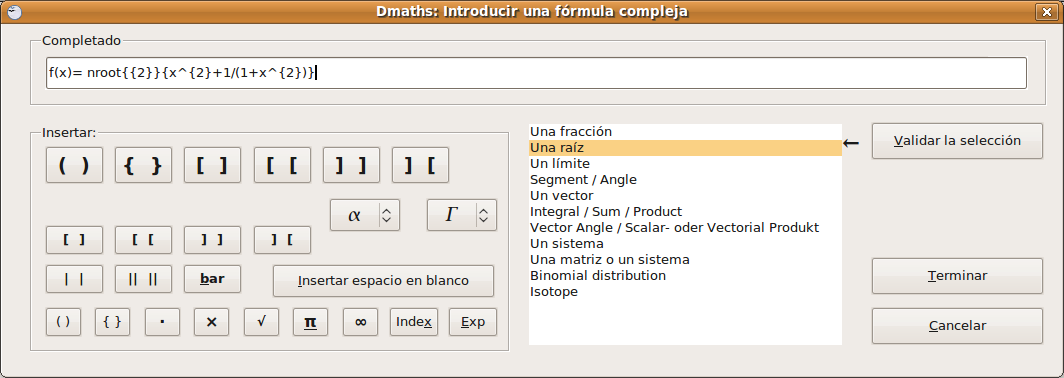 Podemos Terminar ya y nos incluye la siguiente función:
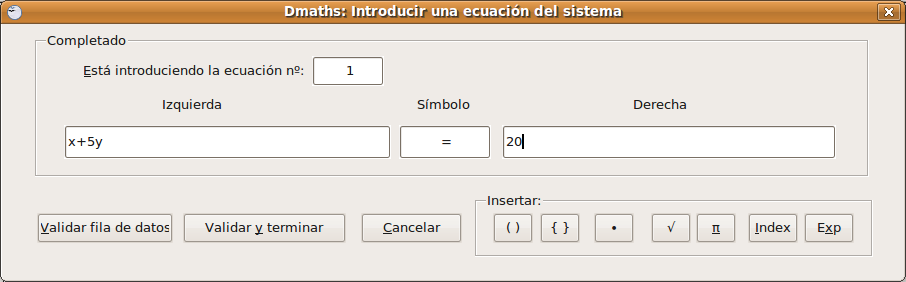
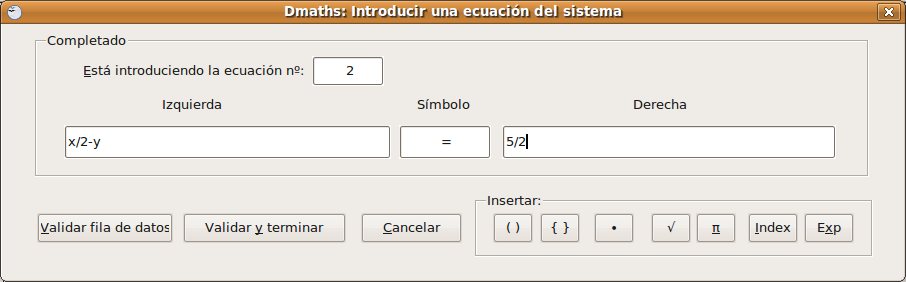
Escribir un sistema de ecuaciones
Para cerrar el sistema pulsamos en Validar y terminar. El sistema creado se incluye en el propio texto, tal y como vemos abajo:
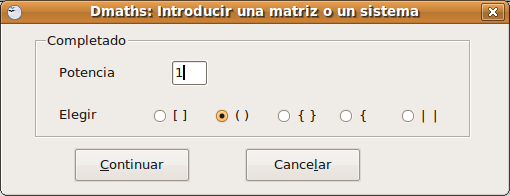
Escribir una matriz 3x3 Pulsar en Crear una matriz y muestra la ventana:
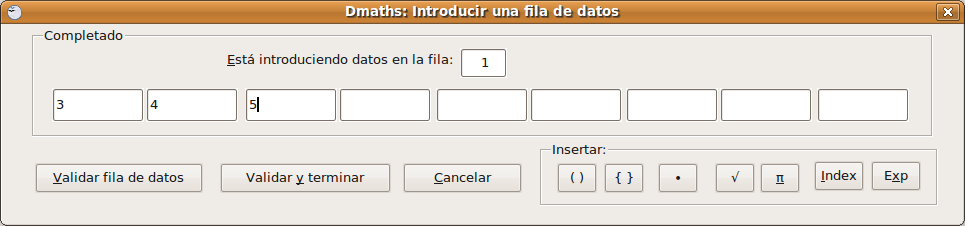
Introducimos la potencia y el tipo de carácter que encerrará la matriz. Pulsamos en Continuar y pide los datos de la primera fila:
De la misma forma para las filas 2 y 3. Pulsamos en Validar y terminar y nos incluye en el texto la matriz siguiente:
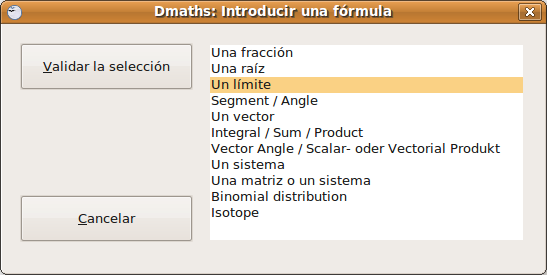
Escribir un límite Seleccionar en la barra de herramientas la opción Crear una fórmula y muestra:
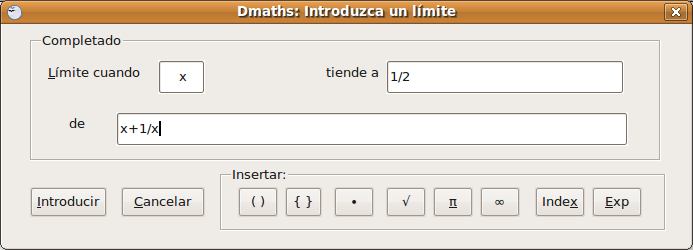
Validamos la selección de Un límite y muestra la ventana donde introduciremos los datos del límite:
Al pulsar en Introducir incluye el siguiente límite:
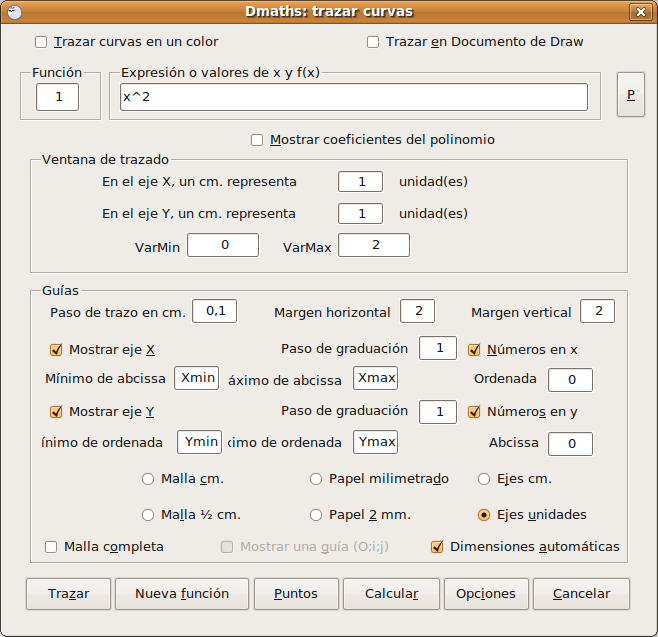
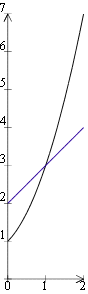
Trazar curvas definidas por una función Pulsamos en Plot a curver y muestra una ventana de opciones en la que damos la función que queremos que dibuje. Para hacerlo sencillo vamos a dibujar la función que viene por defecto. Pero el usuario puede introducir la función que le interese.
Vemos que se trata de una función parabólica que pasa por el origen de coordenadas y no hemos modificado ningún parámetro dado. Ahora podemos ya Trazar la curva o introducir una nueva función para que se dibujen juntas y ver si tienen puntos de corte. En nuestro caso trazamos ya:
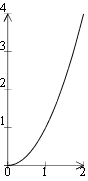
Veamos ahora el caso de dos funciones, una parabólica (x²+x+1) y una recta (x+2):
Utilización de la rejilla Si el profesor necesita que los alumnos trabajen los ejercicios sobre papel milimetrado, dmaths permite crear el papel milimetrado mostrando una rejilla como la siguiente:
En este caso hemos puesto 2mm. Ayuda de dmathsComo vemos Dmaths es un editor de fórmulas matemáticas muy avanzado y potente. Abarca muchos niveles educativos de matemáticas y requiere de adiestramiento para conocer su forma de trabajo. Se recomienda acceder a la opción de ayuda Dmaths > Help y visitar los enlaces incluidos en los que hay disponible información sobre el uso de la extensión. Es también interesante visitar la entrada de Dmaths > FAQs que incluye numerosas cuestiones planteadas y ya resueltas. La opción Dmaths > References muestra un HOWTO algo anticuado (2003) pero que constituye una completa referencia de comandos de fórmulas disponibles. Por último, ir a la página oficial del proyecto a la sección de Documentación (http://www.dmaths.org/documentation/doku.php?id=start), donde el usuario encontrará toda la información relativa a la extensión así como manuales de usuario donde se explican los detalles de su utilización. ConclusiónComo vemos dmaths es un herramienta interesante para el profesor de matemáticas que tenga que escribir a menudo fórmulas o dibujar funciones en sus hojas de ejercicios. Al ser una extensión de OpenOffice.org se integra perfectamente en la suite ofimática, su configuración es mínima y sólo requiere algo de práctica en su uso. Es importante hacer notar que es una herramienta diferente a Openoffice.org Math que también funciona como editor de fórmulas, pero no tiene la potencia de esta extensión. SPIP1 es un sistema de publicación para Internet particularmente atento a un funcionamiento colectivo, al multilingüismo y a la facilidad de uso. Es un software libre, distribuido bajo licencia GNU/GPL. Utilizable para cualquier sitio Internet, ya sea asociativo o institucional, personal o comercial.(http://www.spip.net).
GEOGEBRAIntroducciónEn este artículo vamos a estudiar una aplicación que permite trabajar con geometría dinámica, álgebra y cálculo utilizando el ordenador. Se llama Geogebra y su objetivo es ser una alternativa para la docencia en geometría, álgebra, etc, de forma integrada, dinámica y atractiva para el alumnado. Es una aplicación de software libre, creada por Markus Hohenwarter desde el departamento de Didáctica de la Matemática de la Universidad de Salzburgo y que ha recibido varios premios o reconocimientos, entre ellos el European Academic Software Award (2002), el International Free Software Award, categoría de educación (2005) y el Distinguished Development Award otorgado por la Association for Educational Communications and Technology de Orlando (2008), entre otros. La página web del proyecto es http://www.geogebra.org. Geogebra: característicasLa última versión disponible es la 3.2. Se trata de software libre con licencia GPL para cualquier uso no comercial (http://www.geogebra.org/download/license.txt). Relacionada con Geogebra su uso y difusión es de interés la siguiente wiki en español http://www.geogebra.org/en/wiki/index.php/Spanish. Existen versiones para Windows, Mac OS y GNU/Linux (32bit/64bit). Nosotros vamos a utilizar la versión para GNU/Linux 32 bit. Los ejercicios construidos (construcciones utilizando la terminología de Geogebra) son portables, además de permitir a partir de ellas generar páginas web dinámicas. Geogebra ejecuta un archivo Java (geogebra.jar) y almacena cada uno de los ejercicios o construcciones en un archivo XML con de extensión ggb. Podemos decir que Geogebra está formada por un conjunto de objetos básicos, un conjunto de acciones elementales a realizar sobre estos objetos, un lenguaje de programación que utiliza una sintaxis específica y una interfaz gráfica que permite trabajar, operar y relacionar estos objetos. Desde esta interfaz dinámica e interactiva, los usuarios pueden diseñar, programar y ejecutar acciones y obtener resultados matemáticos del tipo gráficos (interactivos), cálculos, simulaciones, etc. Las principales características de Geogebra son:
Instalación y configuraciónInstalación Existe un paquete .deb de Geogebra para ser instalado en Ubuntu 9.10 Jaunty. Los pasos a seguir para la instalación son los siguientes:
Pero la versión que proporciona este paquete es la 3.0. Si preferimos trabajar con la última 3.2 deberemos hacerlo con el archivo GeoGebra-Linux-Portable-3.2-42-0.tar.gz que descargamos desde http://www.geogebra.org/cms/es/installers.  En este caso los pasos a seguir son los siguientes:
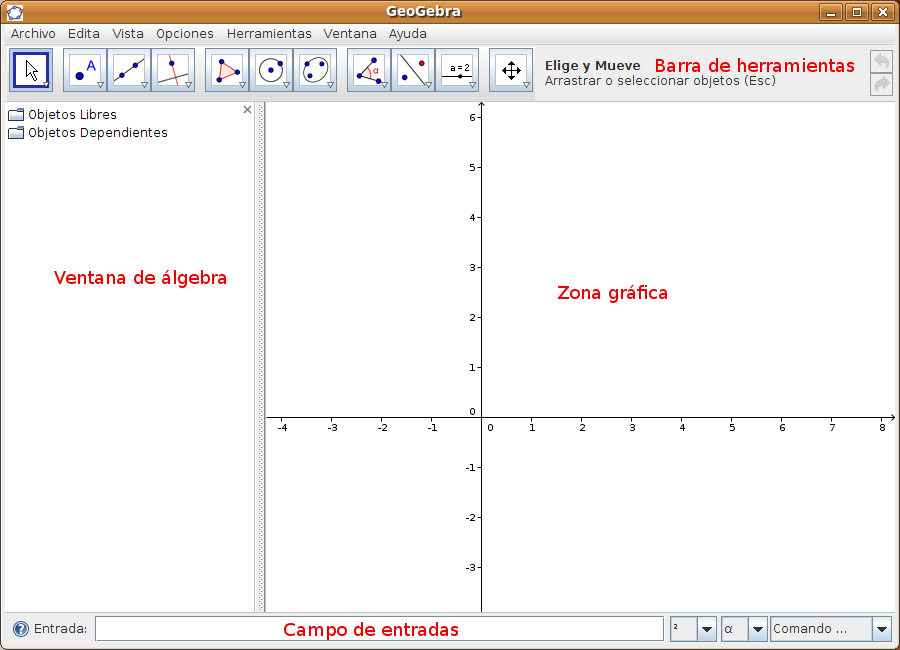
Las zonas de trabajo disponibles son:
Existe aún una zona llamada de Hoja de cálculo. En esta zona o vista cada celda se identifica por su fila y columna. Por ejemplo A1 es la celda situada en la fila 1 columna A. Este nombre puede utilizarse en expresiones u órdenes haciendo referencia a su contenido. En las celdas se pueden incluir números, coordenadas de puntos, funciones, etc y si tienen correspondencia gráfica se verá en la zona gráfica. Tipos de objetos En la zona de álgebra vemos que hay dos tipos de objetos matemáticos:
Tipos de construcciones
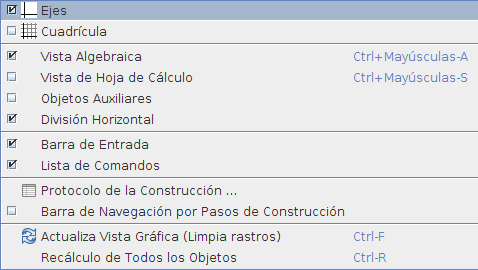
Personalización de la interfaz de usuario Desde el menú Vista se puede mostrar u ocultar las vistas y otros elementos de la interfaz gráfica:
En el menú Vista podemos activar la Barra de Navegación por Pasos de Construcción que incluye al pie de la vista gráfica un botón de reproducción de los diferentes pasos que realizado para la construcción.
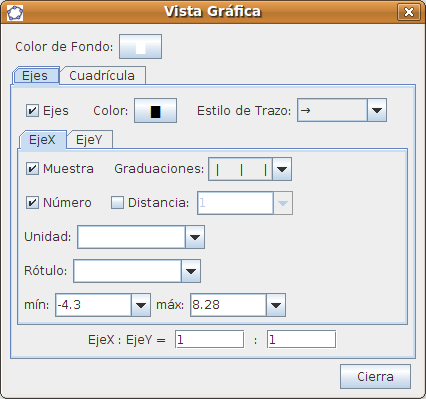
En Opciones > Vista Gráfica podemos establecer los parámetros que determinan los ejes X e Y y su color así como las características de la cuadrícula.
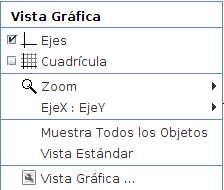
El menú contextual en la vista gráfica incluye una herramienta de zoom de aproximación y alejamiento:
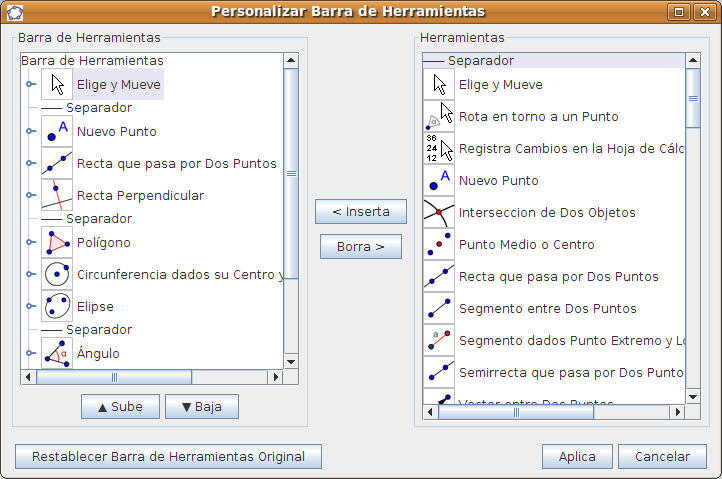
La Barra de Herramientas se puede personalizar desde el menú Herramientas > Personalizar Barra de Herramientas:
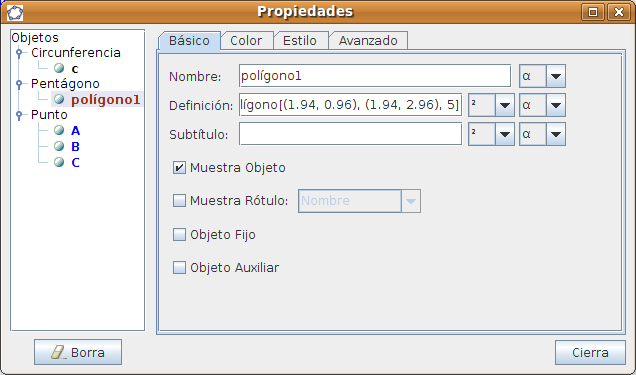
Propiedades de los objetos El usuario puede conocer y actuar sobre las propiedades de los objetos que va creando. Para ello se puede situar tanto en la zona gráfica como en la de álgebra y pulsando el botón derecho seleccionar Propiedades:
En este caso vemos las propiedades de un polígono: nombre, datos de su construcción y podemos establecer su estilo de trazo, color, etc. Instalación de javaGeoGebra requiere tener instalado en el ordenador Java. Podemos comprobar si nuestro ordenador ya dispone de Java accediendo a la página http://www.java.com y ejecutando el test de comprobación. Desde esta página también se puede descargar la versión para Ubuntu junto con el manual de instrucciones para su correcta instalación (http://java.com/es/download/linux_manual.jsp).
Nos descargamos la versión para Linux (archivo autoextraible) jre-6u20-linux-i586.bin. Para instalar:
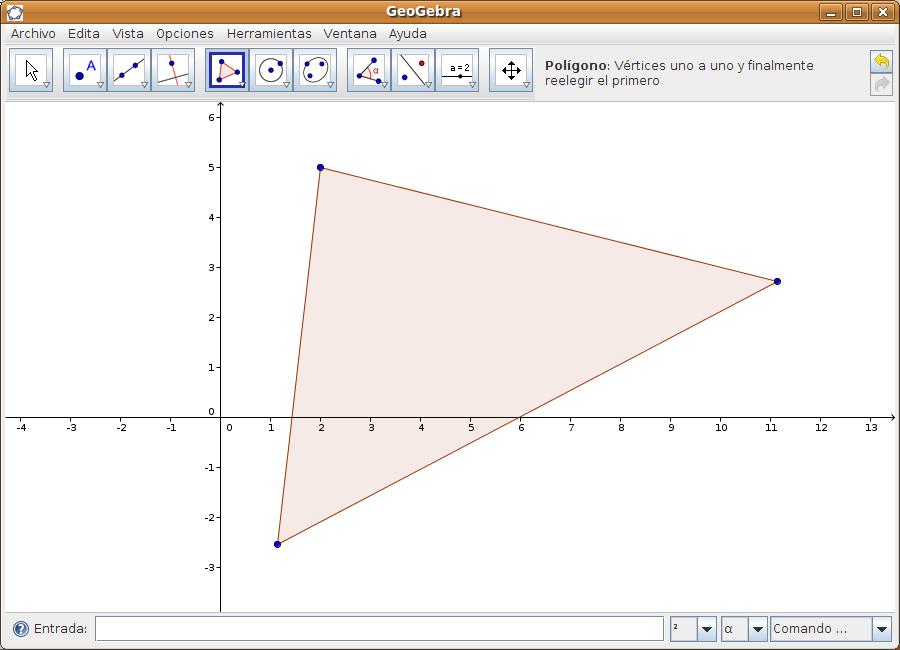
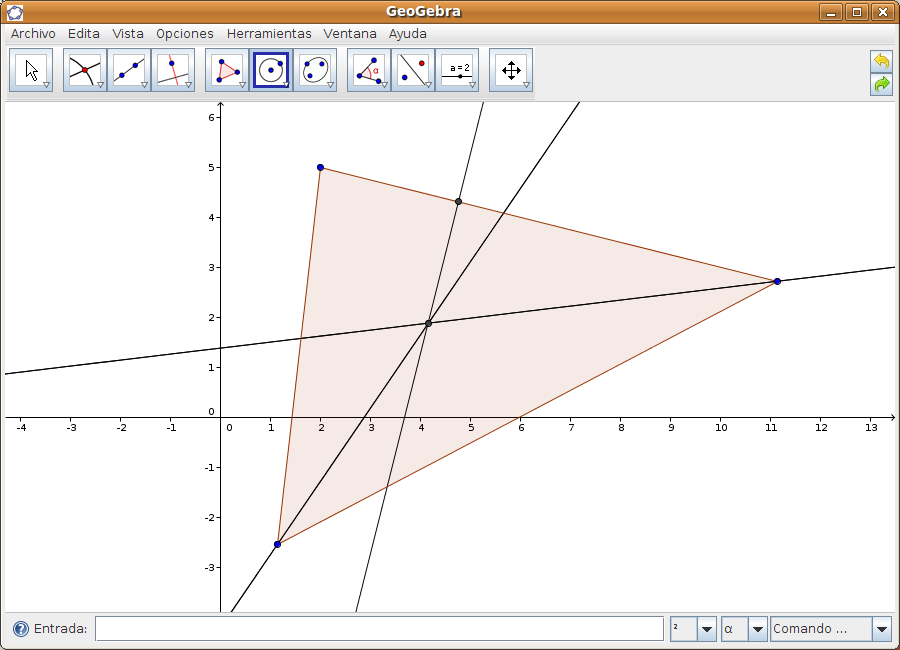
Utilización de Geogebra: casos prácticosPartimos del supuesto de que la práctica es la mejor forma de evaluar la herramienta. Por ello, vamos a estudiar el funcionamiento de Geogebra mediante la realización de varios casos prácticos, todos ellos muy sencillos. Caso 1Vamos a dibujar la circunferencia inscrita en un triángulo cualquiera. Paso 1 Cerramos la ventana de Álgebra. En la zona gráfica seleccionamos la función Polígo
Paso 2 Dibujamos las bisectrices de dos de los tres ángulos S Seleccionamos el punto de intersección de ambas bisectrices y calculamos la perpendicular desde este punto de intersección hasta el lado opuesto.
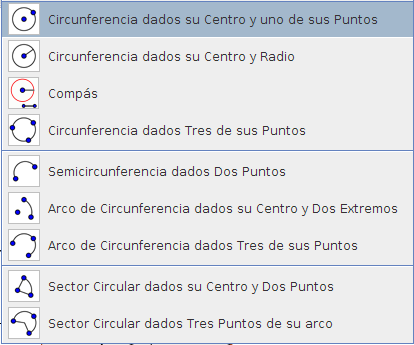
Paso 3 Dibujo de la circunferencia inscrita Seleccionamos la opción marcada en:
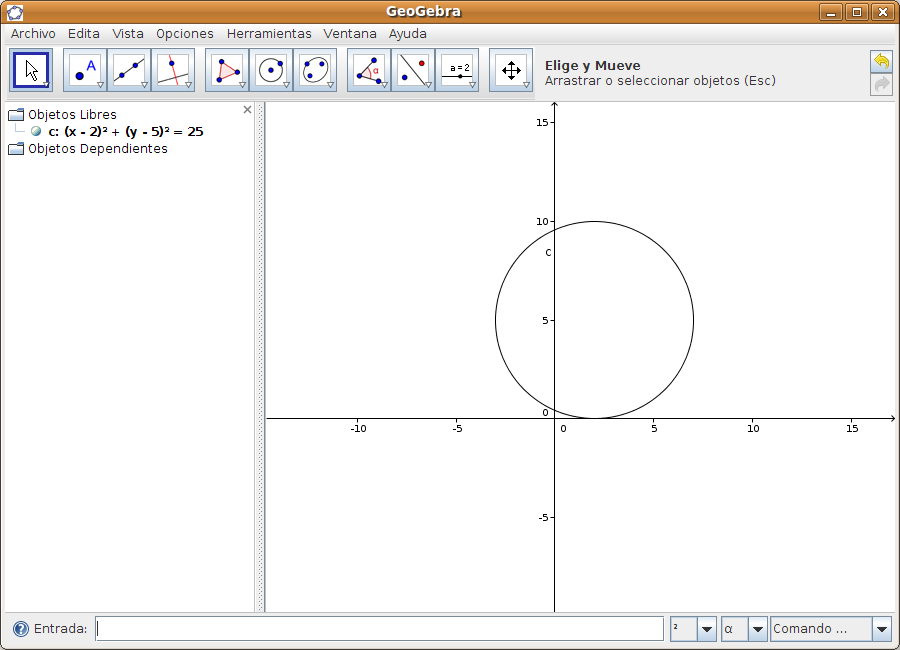
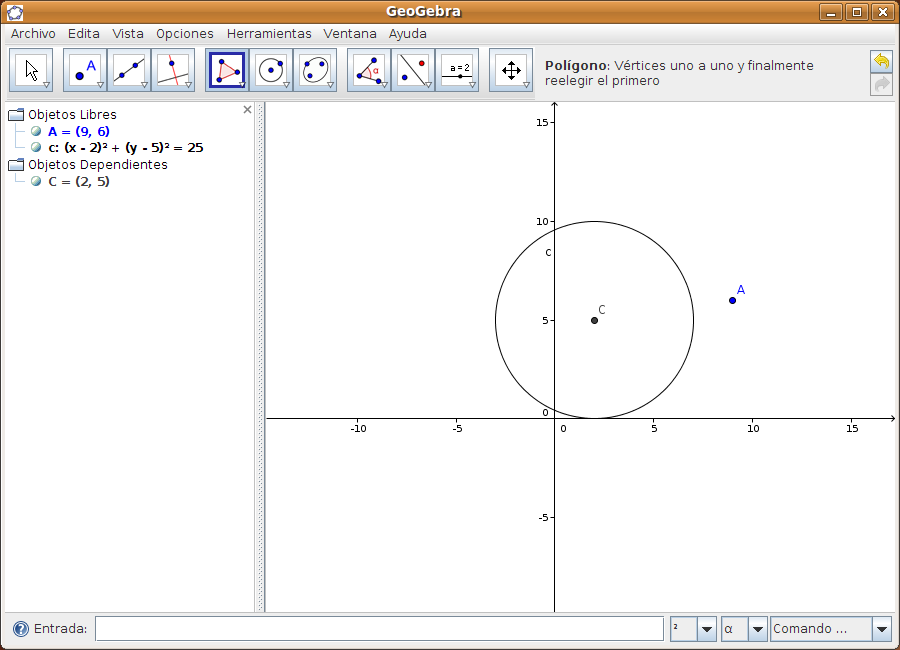
Guardar la construcción desde Archivo > Guardar como. Caso 2Tenemos la ecuación de la circunferencia c (x - 2)² + (y - 5)² = 25 y queremos representar tanto la circunferencia como sus tangentes que pasan por el punto A de coordenadas (9, 6). Paso 1 Introducir la ecuación de la circunferencia (x - 3)² + (y - 2)² = 25 en la zona de entradas y pulsar INTRO.
Paso 2
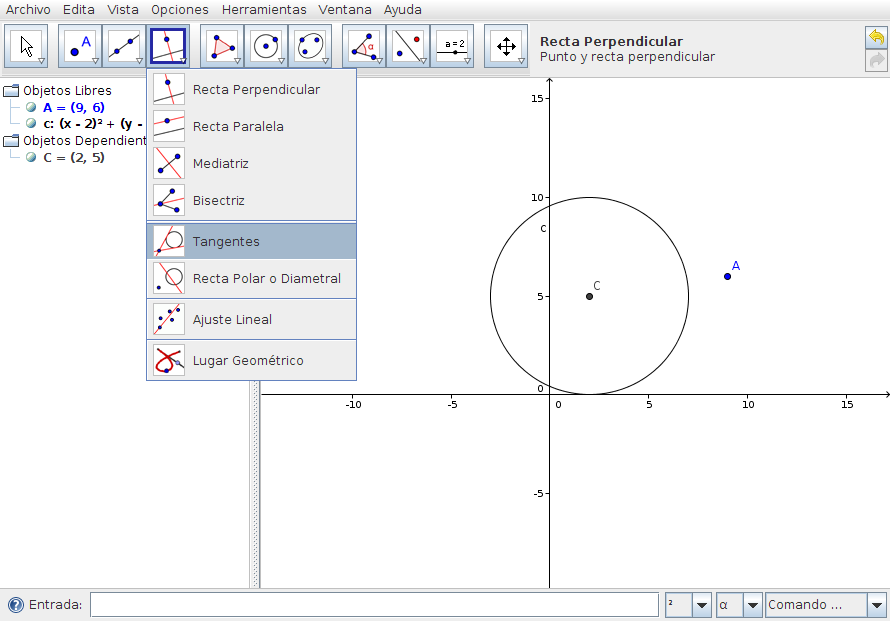
Paso3 Ir a la Barra de Herramientas y desplegar el cuarto icono. Seleccionar el modo Tangentes y hacer clic sobre el punto A y sobre la circunferencia c.
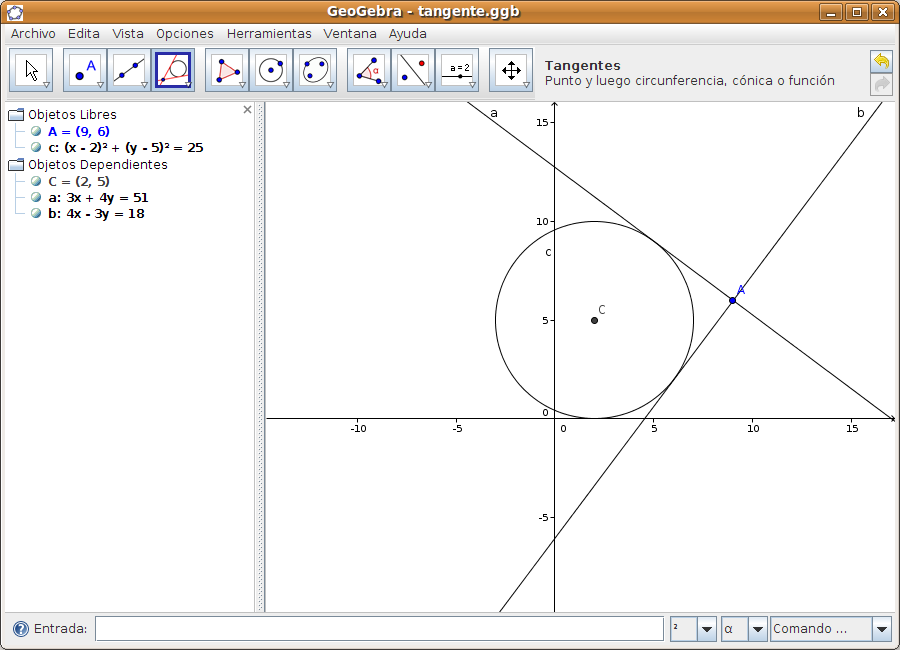
Esperamos unos segundos y se dibujan las dos tangentes, al tiempo que en la zona de álgebra aparecen las ecuaciones de las dos rectas tangentes que se han dibujado.
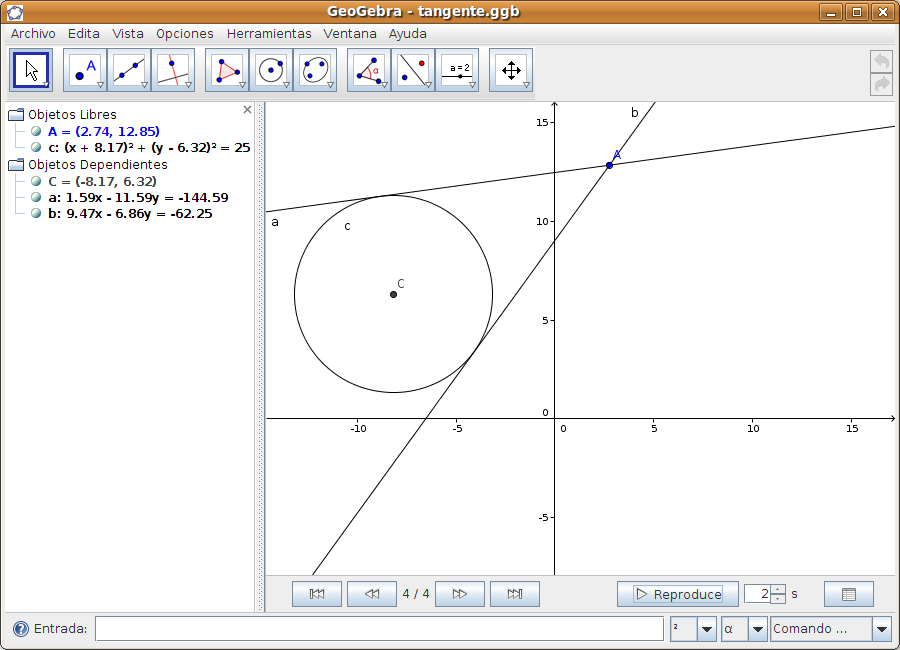
Paso 4 Utilizamos el botón de desplazamiento En este paso vamos a comprobar como se actualizan las diferentes zonas en función de donde se hagan las variaciones. Por ejemplo, desplazamos la circunferencia y... observamos que las tangentes se adaptan.
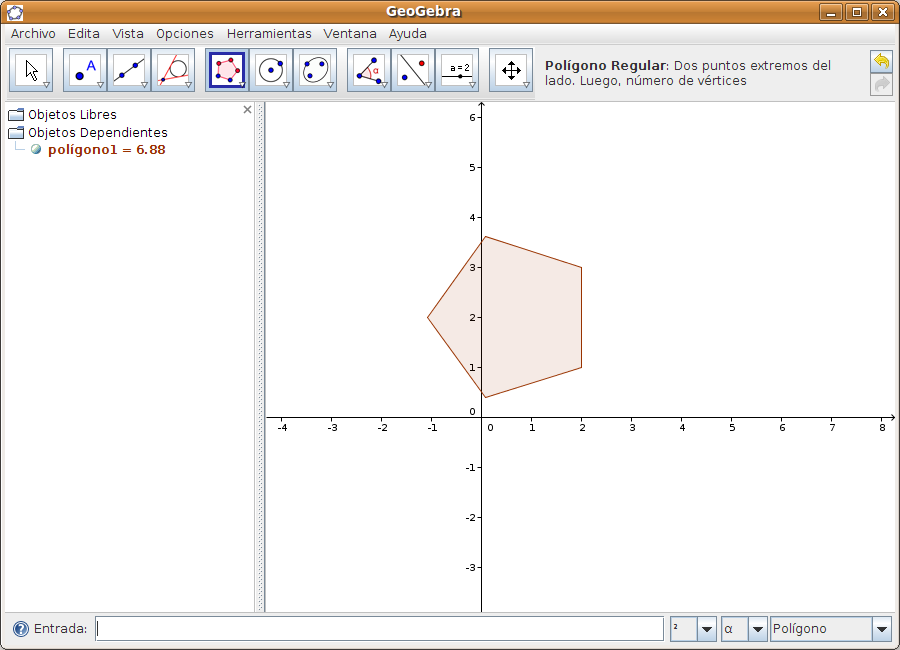
También podemos mover el punto A y comprobar como se mueven las tangentes. Hemos incluido también la barra de reproducción para ver en secuencia los pasos realizados en la construcción. Salvar los cambios si se quieren. Caso 3Vamos ahora a dibujar un pentágono y su circunferencia circunscrita. Paso 1 Dibujamos e pentágono En primer lugar vamos a Archivo > Nuevo para comenzar un nuevo trabajo. En la barra de herramientas seleccionamos el botón Polígono regular En la zona de entradas y comandos, localizamos la orden Polígono. Los datos que requiere esta orden son un punto (a,b) extremo de un lado del polígono, otro punto (a,b) para el otro extremo del lado y el nº de lados del polígono. Los datos dados por nosotros en la fórmula son:
Al pulsar INTRO se dibuja nuestro pentágono.
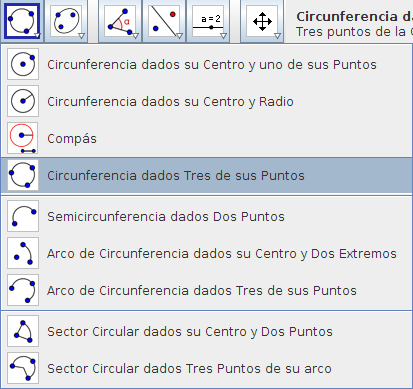
Paso 2 Búsqueda del centro de la circunferencia circunscrita Como se trata de un polígono regular, si tomamos 3 vértices del pentágono, por ellos pasará la circunferencia circunscrita. Buscamos la función correspondiente:
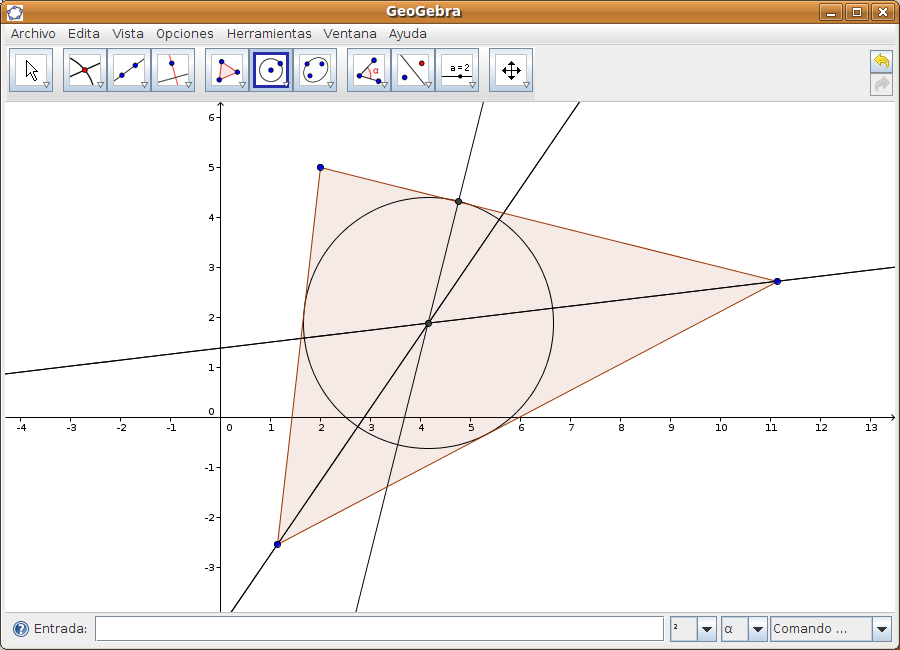
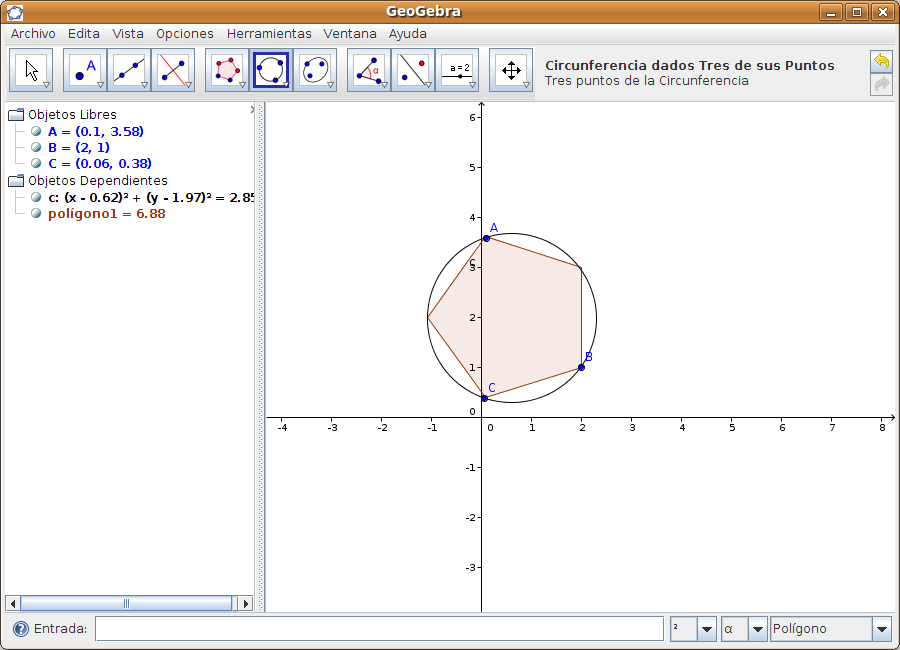
Seleccionamos la opción Circunferencia dados Tres de sus Puntos, y con el ratón marcamos los 3 vértices que queramos. Se dibuja la circunferencia:
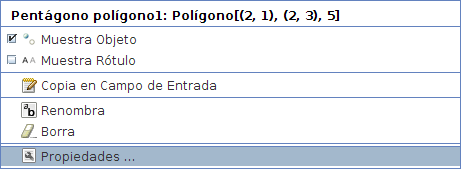
Paso 3 Seleccionamos el modo Desplaza y Esto es lo que llamamos la Geometría dinámica. Todos los objetos tienen sus Propiedades. Para conocerlas estando sobre el objeto, pulsar el botón derecho del ratón y el menú contextual nos muestra:
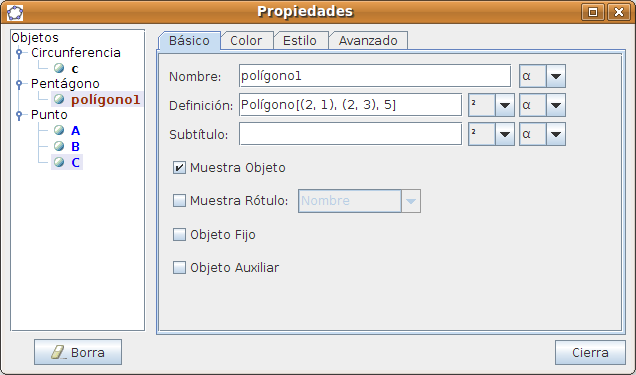
Seleccionamos la entrada Propiedades y muestra una ventana con propiedades configurables del polígono:
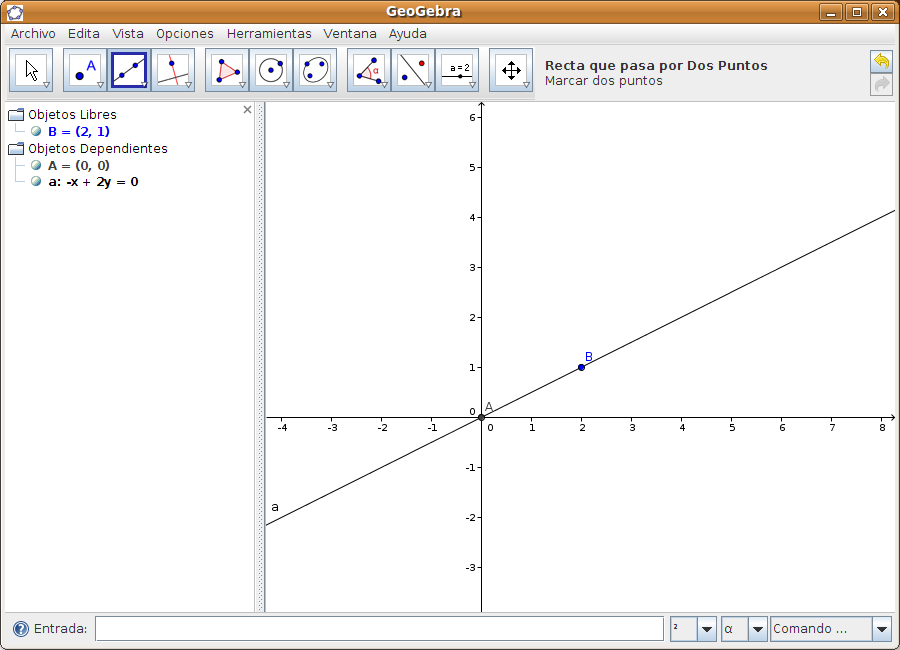
Las diferentes pestañas nos permiten poner subtítulo al objeto, mostrar un rótulo, cambiar los colores, el grosor y estilo del trazo, etc Caso 4 Estudio de funciones lineales f(x)=axPaso 1 Dibujamos una recta que pasa por dos puntos: A(0,0) y B(2,1). Para ello pulsamos en La figura siguiente muestra gráficamente la recta y en la zona de álgebra la ecuación correspondiente:
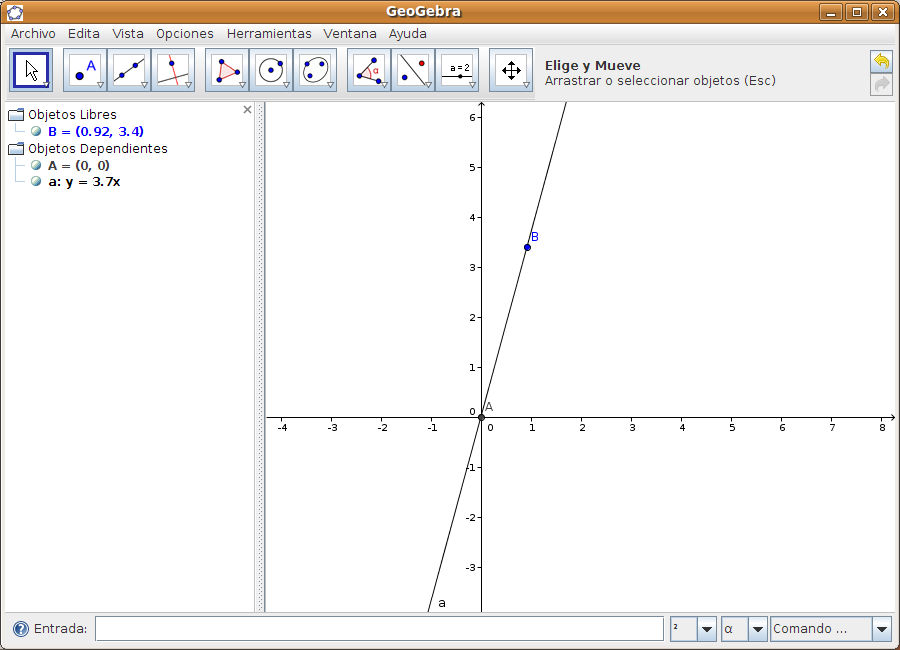
Paso2 Situamos el ratón sobre la recta y en el menú contextual seleccionamos las Propiedades. Vamos a la pestaña Álgebra y cambiamos la ecuación de la recta a y=ax+b para poder estudiar las variaciones en la pendiente de la recta. Si ahora hacemos clic en el botón de desplazamiento y pulsamos sobre el punto B, que es el objeto libre, veremos como cambia la ecuación de la recta al ir cambiando la pendiente de la misma.
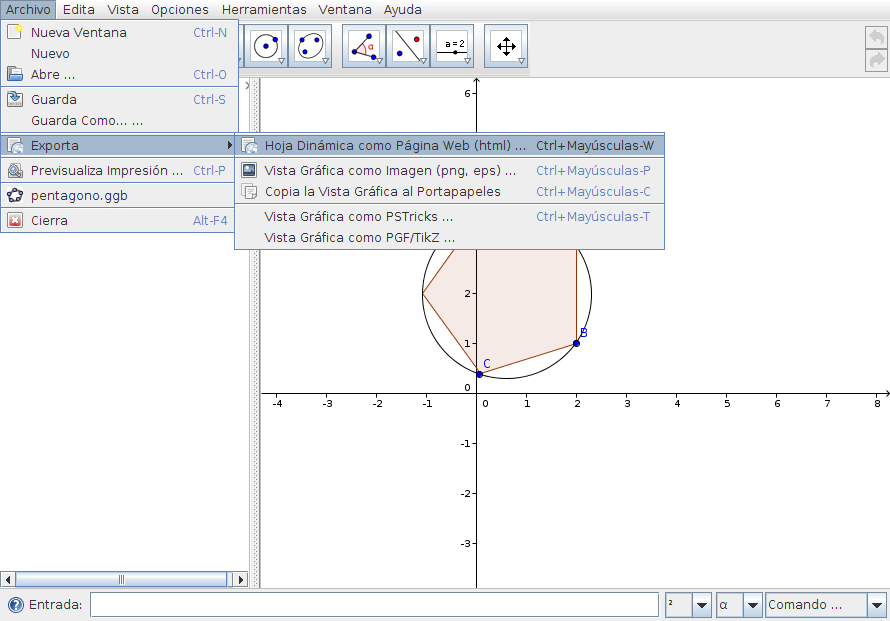
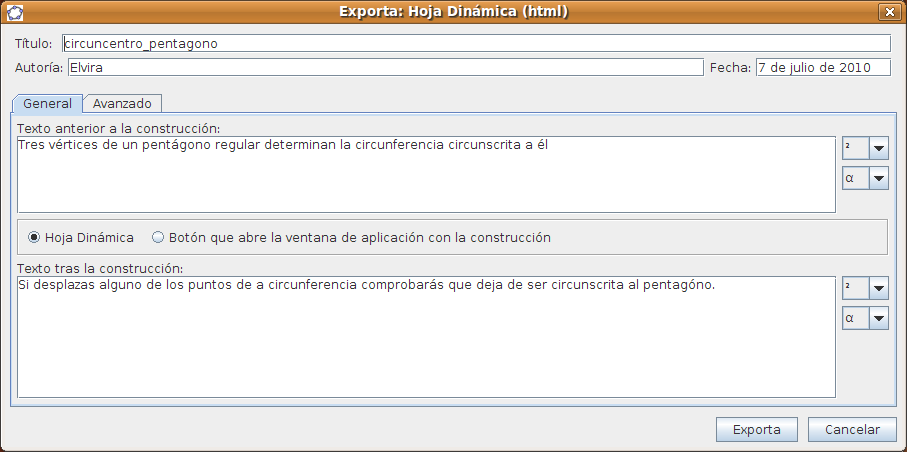
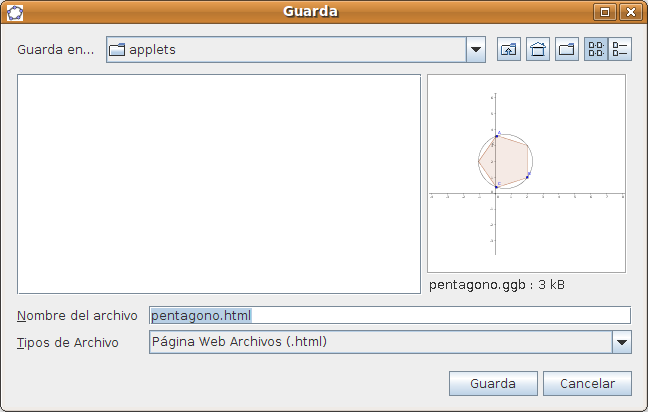
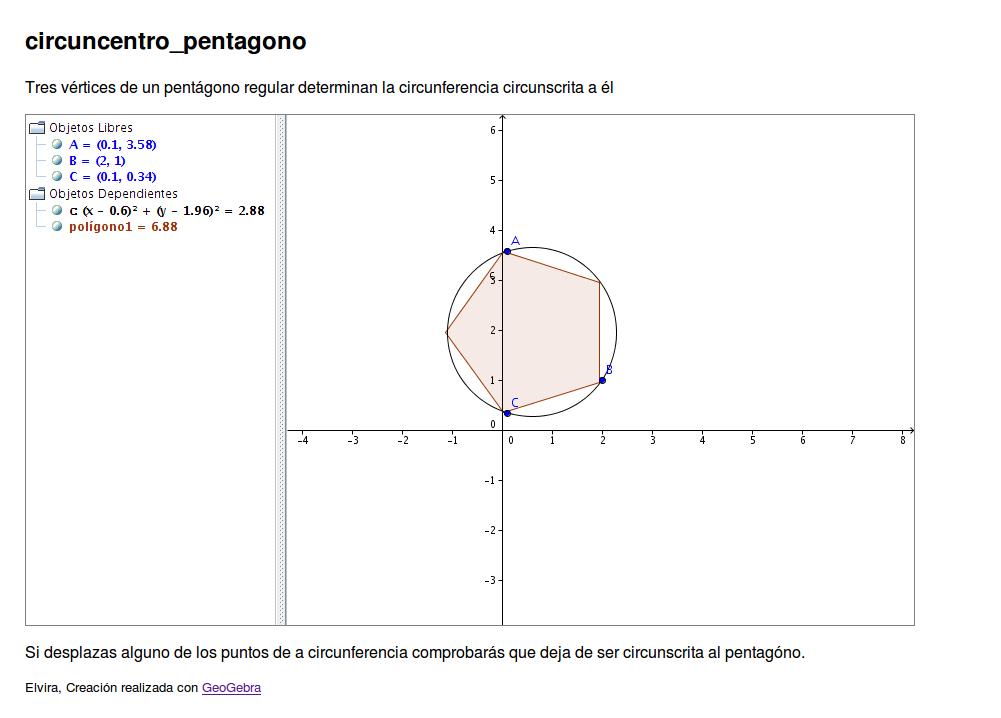
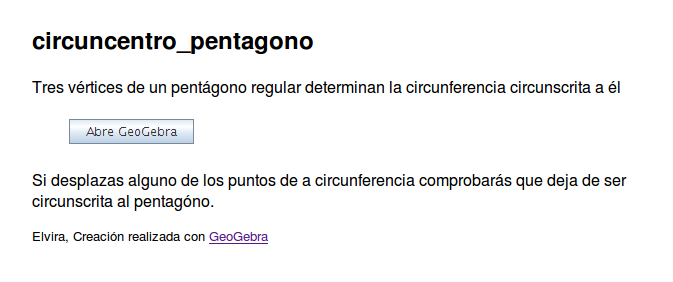
Creación de applets con GeogebraA partir de un dibujo elaborado con Geogebra podemos generar un applet1 que insertaremos en una página web. Elaborar estos dibujos con Geogebra ya hemos visto que es muy sencillo y la generación del applet es automática. Además no pierden la interactividad, como las construcciones que hemos realizado en los casos prácticos. Pasos para crear un appplet con Geogebra
ConclusiónRealmente hemos realizado una descripción muy breve de Geogebra, pero suponemos que se ha podido intuir el potencial que tiene y la gran ayuda que supone para el profesor de Matemáticas interesado en la introducción de las TIC en el aula. Geogebra es mas que un digno rival de Cabri (software educativo y propietario para trabajar con geometría dinámica, http://www.cabri.com/es/) y su difusión es muy grande. Existen numerosas comunidades de usuarios de Geogebra que a través de sus foros, celebración de Jornadas, etc, producen y mantienen numerosa documentación relacionada con el uso de Geogebra en el aula. En concreto desde el ITE (Instituto de Tecnologías Educativas) se ofrece en su sección de Formación en Red, un DVD con experiencias basadas en Geogebra (http://www.isftic.mepsyd.es/formacion/enred/experiencia/index.php) preparadas por los propios profesores que han realizado el curso correspondiente. Enlaces de interés
1En general un applet es un componente de una aplicación que se ejecuta en el contexto de otro programa, por ejemplo un navegador web. En particular el Java applet es código Java utilizado en una página HTML y representado por una pequeña pantalla gráfica dentro de ésta.(http://es.wikipedia.org/wiki/Applet).
gMatESOIntroducciónExiste una gran variedad de aplicaciones dentro del Software Libre, dedicadas a facilitar al profesor de matemáticas su tarea en el aula. Algunas de ellas son sumamente amplias, completas pero también complejas. En este monográfico estamos presentando un grupo de aplicaciones muy sencillas de instalar, configurar y utilizar, que pueden ayudar al profesor tanto a impartir sus clases, como a preparar exámenes. Una de ellas es gMatESO, creada por Daniel López Avellaneda y bajo licencia GNU/GPL. Se trata de una aplicación que tiene dificultad 'cero' en cuanto a su instalación, configuración y uso. Sin embargo es una herramienta que el profesor puede utilizar en el aula como complemento a sus explicaciones y el alumno para comprobar si el resultado de sus cálculos con número naturales y fracciones son correctos. gMatESO: características y requisitosCaracterísticas Básicamente gMatESO consiste en una colección de fichas de matemáticas muy útiles para los alumnos del último curso de Primaria y algunos niveles de la Secundaria Obligatoria. Se diferencia de otras aplicaciones en que detalla los pasos o proceso a seguir hasta conseguir solucionar el ejercicio. Hay que tener en cuenta que, aunque se puede utilizar como calculadora, su objetivo es didáctico y no se debe considerar como un programa de cálculo científico. La versión que se explica en el artículo es la 0.1. Dispone de un sencillo menú con dos opciones
gMatESO permite trabajar con los números naturales y las fracciones. Las operaciones que permite realizar son las siguientes:
Nivel I: después de introducir una fracción permite
Nivel II: después de introducir una pareja de fracciones permite
Nivel III: permite introducir expresiones (sencillas o complejas) combinadas con fracciones (incluyendo signos de operación y paréntesis) calculando el resultado paso a paso. Requisitos gMatESO funciona en equipo que tenga instalado cualquier sistema GNU/Linux y trabaja con el escritorio GNOME con la condición de que la versión sea 2.6 o superior. Podemos averiguar cuál es la versión que tenemos en nuestro equipo ejecutando en una terminal la orden gnome-about. Apenas consume recursos, ya que está formado por un conjunto de pequeños programas ejecutables. Tiene, por tanto, pocos requerimientos de memoria RAM, procesador y de tarjeta gráfica. gMatESO: instalaciónProponemos dos métodos de instalación: Instalación del fuente El archivo fuente se puede descargar desde http://lubrin.org/gmateso/ y se llama gmateso-0.1.tar.bz2. Los pasos a seguir en la instalación son los siguientes:
NOTA: Para que funcione correctamente la aplicación es necesario que la carpeta de gMatESO esté ubicada en el home del usuario (/home/elvira/gmateso-0.1). Instalación del paquete .deb La distribución GNU/Linux LliureX ha empaquetado la herramienta y la pone a disposición del usuario en su pool. Para descargar el paquete hay que modificar los repositorios de Ubuntu añadiendo, como software de terceros, los de LliureX. Para ello ir a Sistema > Administración > Gestor de paquetes Synaptic e introducir la contraseña del usuario sudo. Ir a Configuración > Repositorios: 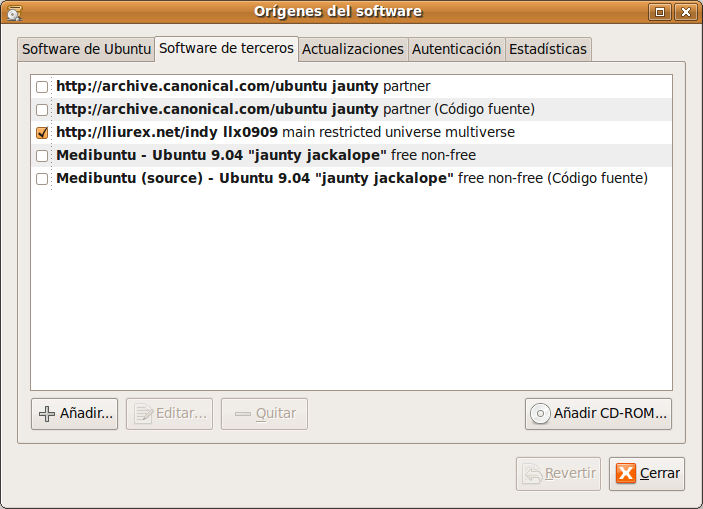 Comprobar que en la pestaña de Software de terceros se ha añadido la línea correspondiente al pool de LliureX de la versión 9.09. Pulsar en Cerrar y nos avisa de que los repositorios han cambiado con lo que hay que pulsar en el botón Recargar para que la lista de paquetes disponibles se actualice.
A continuación buscamos el paquete gmateso y una vez localizado lo marcamos para instalar pulsando el botón derecho. Por último pulsar en Aplicar. 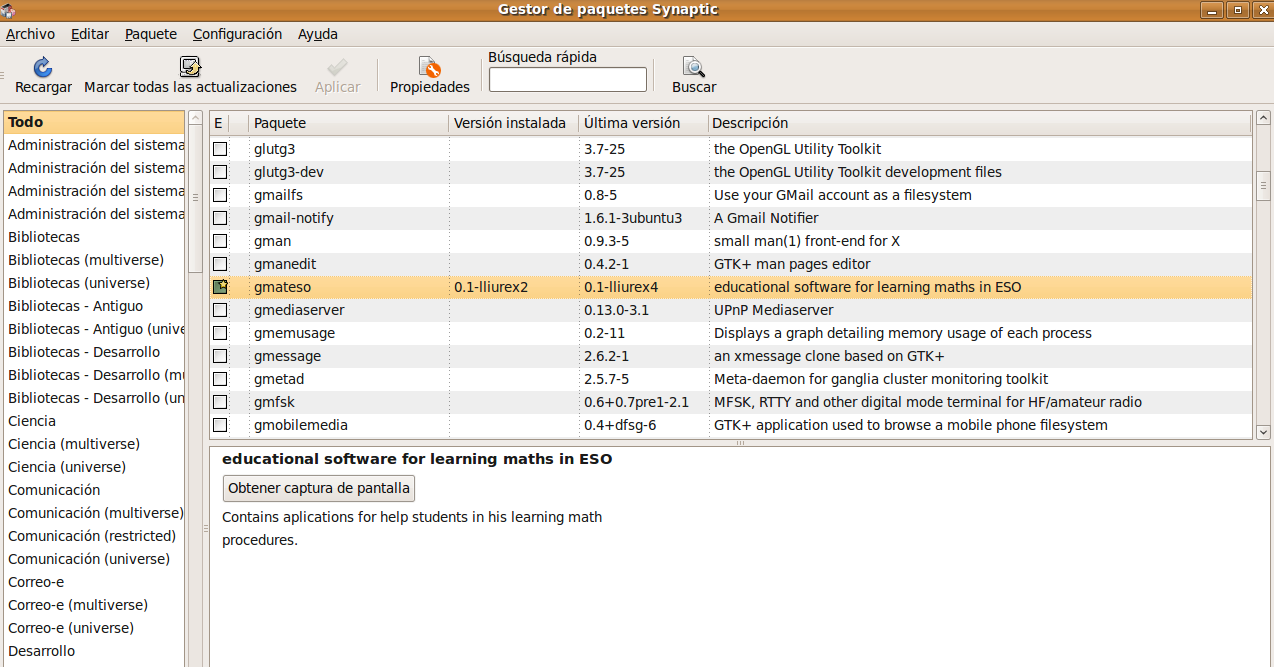 Utilización de gMatESOCon cualquiera de ambas instalaciones para abrir gMatESO vamos a Aplicaciones > Educación > gMatESO. Lo primero que muestra son los créditos de la aplicación indicando los autores:  Cerramos y nos muestra la pantalla de gMatESO. En ella explica la funcionalidad de la aplicación.  Vamos ahora a ver qué nos permite hacer gMatESO y comprobaremos lo sencillo que es operar con ella. Realizaremos diferentes tipos de cálculos referidos a los números naturales y a las fracciones. Naturales¿Cómo obtener los divisores de un número? Para ello indicamos el número del cual se quieren obtener los divisores y pulsamos en Calcular. La figura siguiente muestra la operación: 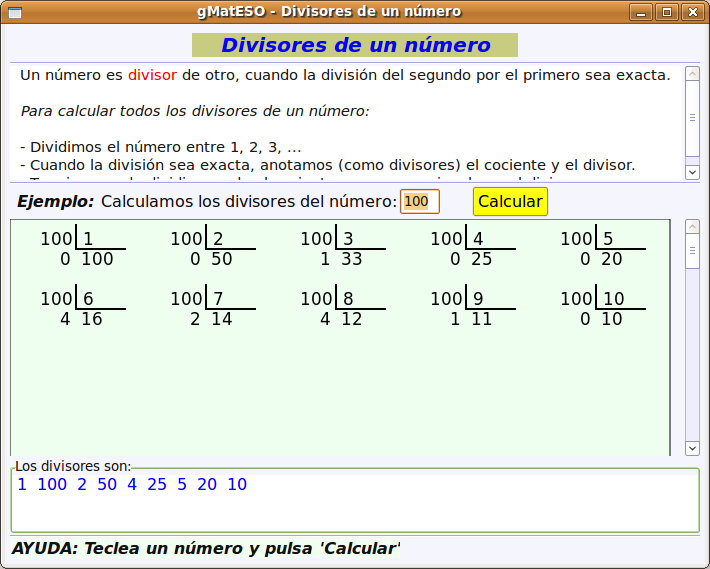 La parte superior de la ventana de cálculo explica el proceso realizado. Para ver completamente dicha explicación es posible que se necesite ir a la barra de desplazamiento de la derecha. Números primos Para su cálculo se utiliza la criba de Eratóstenes, cuyo funcionamiento viene explicado en la cabecera de esta opción de cálculo. La primera figura muestra todos los números desde el 1 hasta el que hayamos introducido para calcular sus primos. En nuestro caso, el 100. 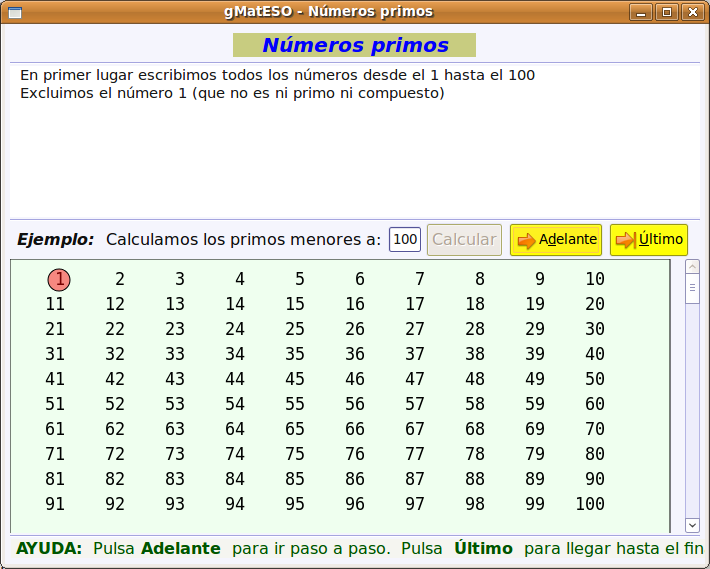 Ahora vamos pulsando sucesivamente el botón Adelante y se van aplicando los criterios de obtención de múltiplos sucesivamente (2 ,3 ,5, …). Los múltiplos que vayamos obteniendo se van tachando de la tabla. 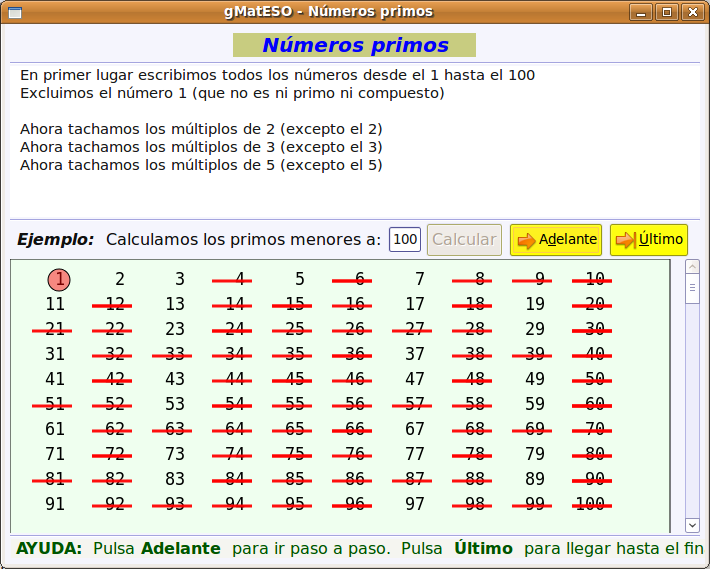 Cuando se llega a la mitad del número dado termina el proceso y se muestran los primos obtenidos (en azul). 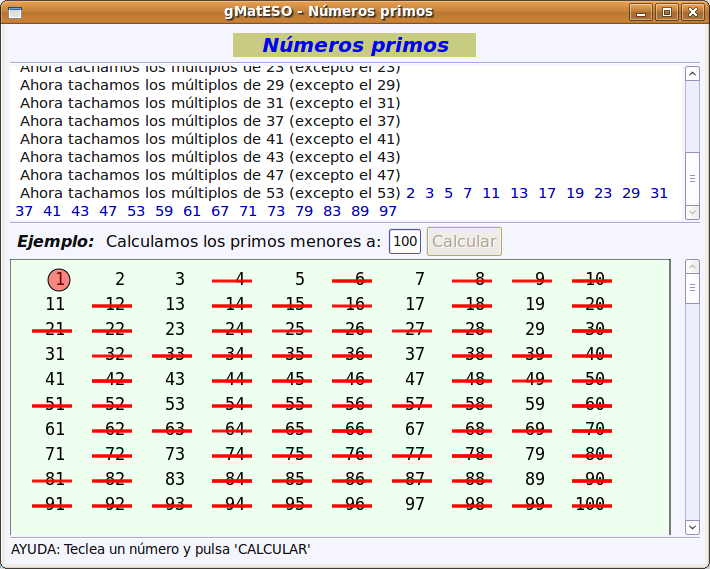 Factorización Introducimos el número natural que queremos factorizar y pulsamos en Factorizar. Observar que en la ventana superior se explica el concepto de factorización y el proceso que se realiza para ello. 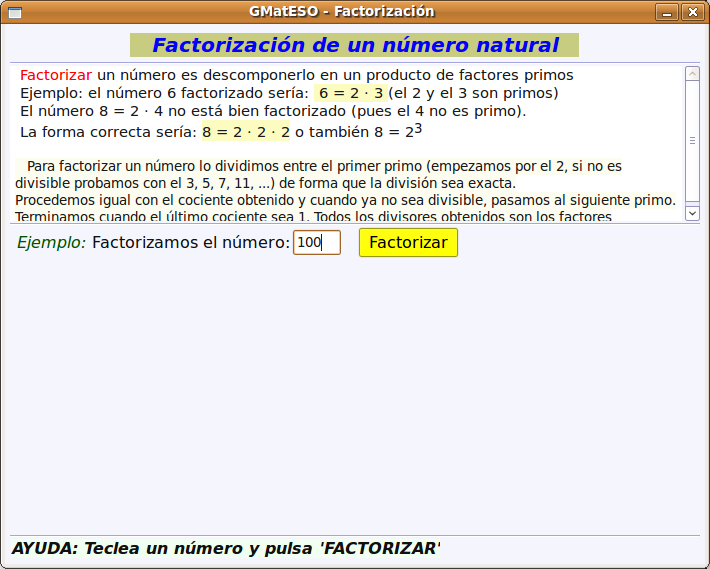 La figura siguiente muestra las descomposiciones obtenidas por el primer número primo que es el 2. 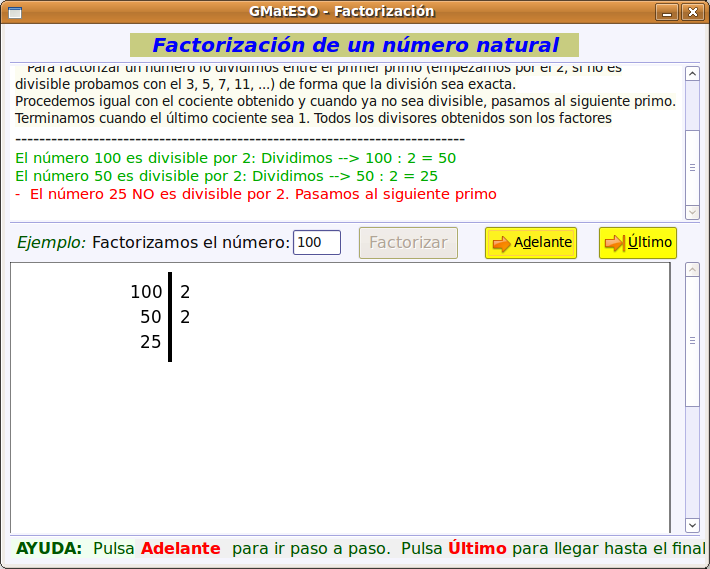 Seguimos pulsando el botón Adelante hasta llegar al último número primo del cual es divisor. En un recuadro azul muestra el número introducido y el resultado de la factorización. 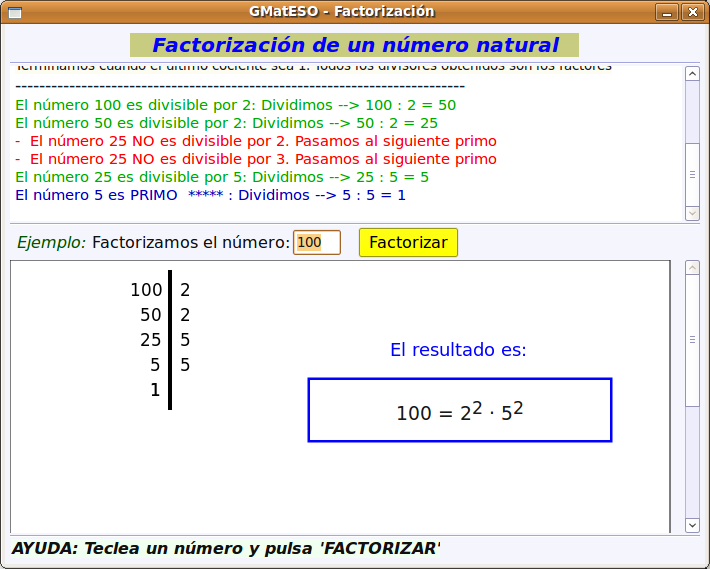 Cálculo del mínimo común múltiplo (mcm) y del máximo común denominador MCD). Introducimos hasta 4 números y pulsamos la opción de cálculo del MCD. 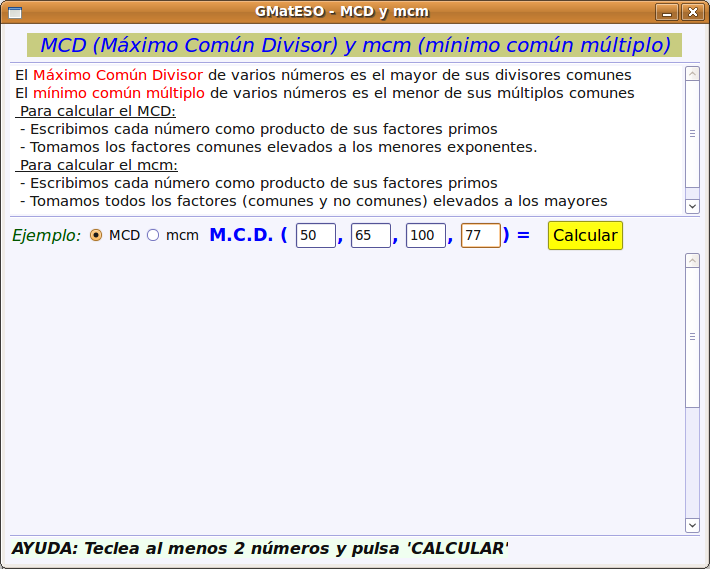 Ahora pulsamos en Calcular realiza la descomposición de los cuatro números y aplica la definición de MCD. En la ventana superior nos muestra el resultado en azul: 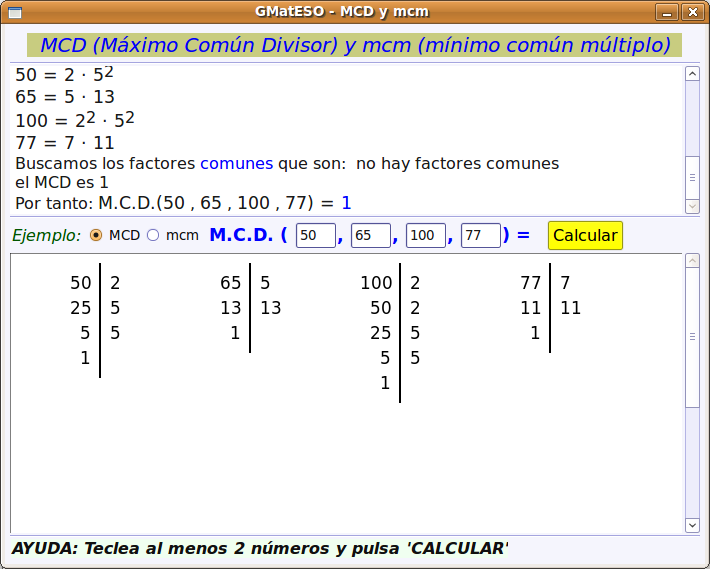 Si queremos obtener el mcm seleccionamos esa opción, introducimos los números y pulsamos en Calcular. FraccionesEn el caso de las Fracciones en primer lugar hay que seleccionar el nivel. El Nivel 1 por ejemplo indica que se trabaja sobre una única fracción. El Nivel 2 trabaja sobre 2 fracciones,... Nivel 1 Introducimos el numerador y el denominador o pulsando el dado se muestra una fracción aleatoria. Pulsar Aceptar y muestra el resultado de la división. 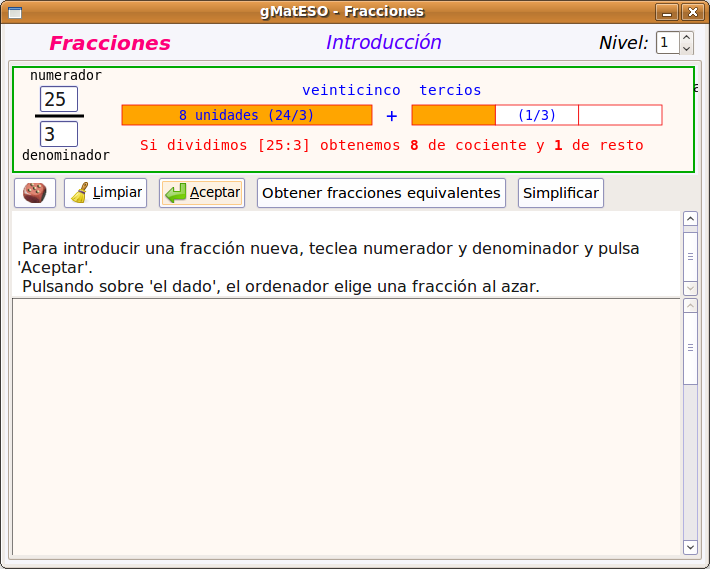 Otras opciones del Nivel 1 es obtener fracciones equivalentes y simplificar la fracción dada. Podemos pulsar en la escoba para Limpiar y probar la opción de Obtener fracciones equivalentes de una fracción al azar. 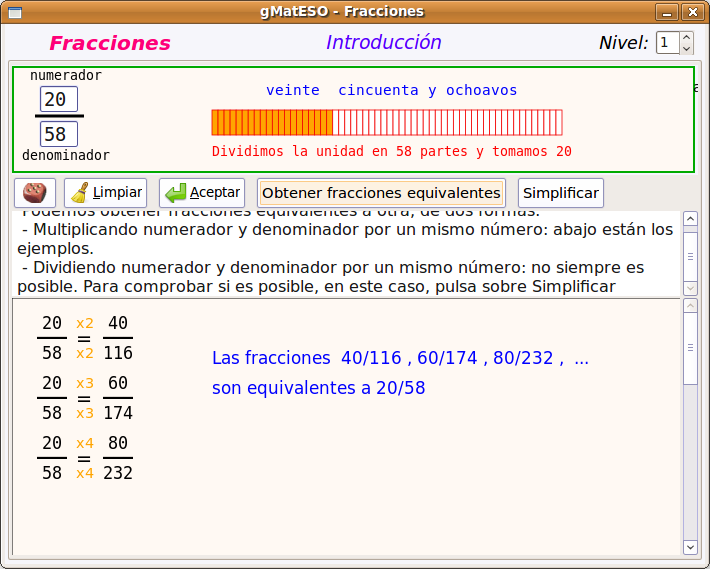 Nivel 2 El Nivel 2 trabaja sobre dos fracciones y permite realizar operaciones entre ellas. Pulsamos el dado y generamos dos fracciones al azar. Ahora hay que seleccionar el tipo de operación que se va a realizar entre ellas. Por ejemplo una suma (+). Por último pulsar en el signo = para obtener el resultado. 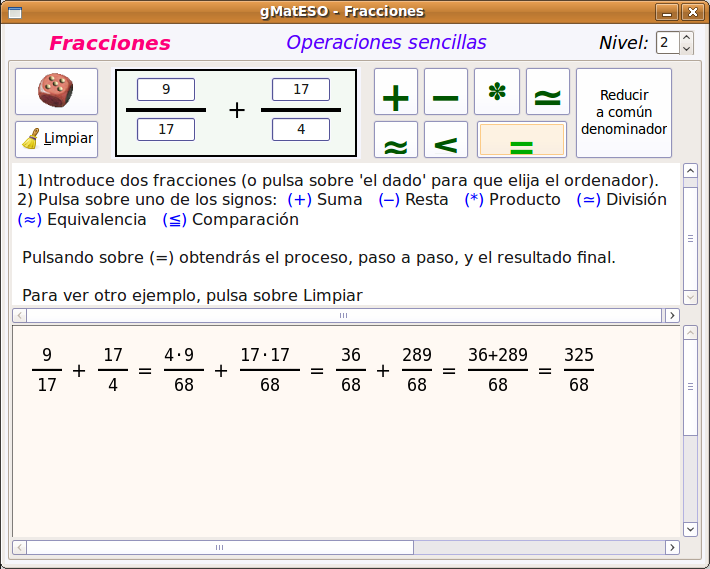 Otro ejemplo de operación entre dos fracciones sería comprobar si son equivalentes. La figura siguiente muestra el procedimiento y el resultado: 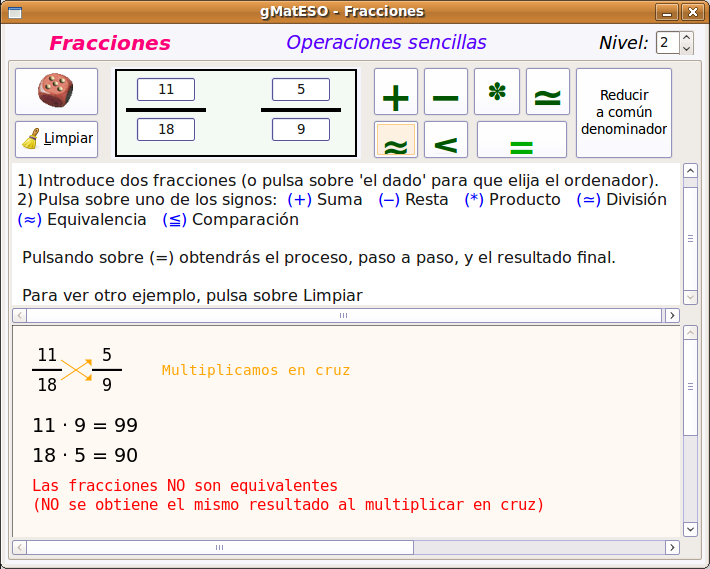 Nivel 3 En el Nivel 3 se trabaja sobre expresiones algebraicas utilizando operaciones combinadas sencillas. Introducimos la expresión todo lo complicada que queramos utilizando los operadores y paréntesis. Al pulsar en Calcular se realizan las operaciones indicadas en diferentes pasos y al final se muestra el resultado. El proceso se muestra en la ventana inferior. 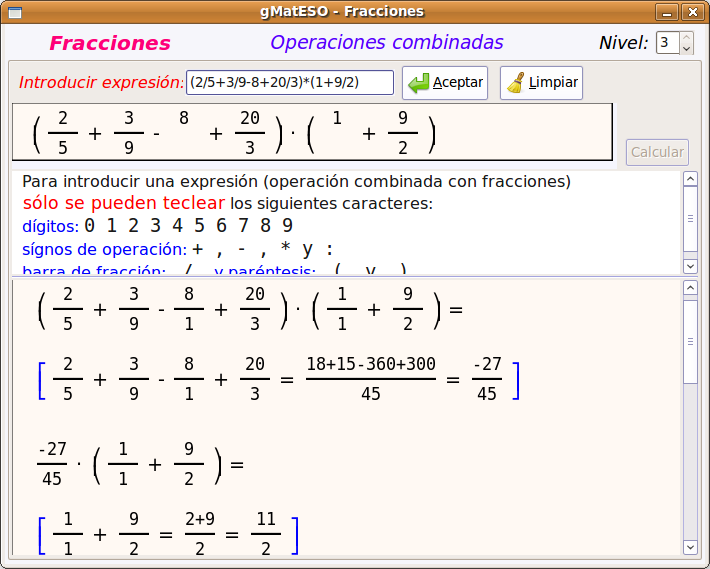 Ayuda de gMatESORealmente gMatESO es una aplicación muy sencilla de utilizar. Pero aún así dispone de una ayuda completa disponible desde la opción de menú Ayuda > Índice. La ventana que despliega contiene información detallada de todas sus posibilidades.  ConclusiónComo vemos gMatESO es un herramienta interesante para el profesor de matemáticas que tenga que iniciar a sus alumnos en las dos áreas curriculares que abarca: los números naturales y las fracciones. Es muy fácil de instalar, no requiere configuración y es de utilización muy sencilla. Lógicamente, de funcionalidad limitada, pero lo que proporciona lo hace de forma completa y simple. Nada que ver con otras aplicaciones matemáticas que ofrecen mucha mayor funcionalidad, pero que son, también, de mayor complejidad en su uso. Bajo nuestro punto de vista un alumno que curse final de Primaria o el primer curso de la ESO, puede trabajar con esta aplicación de forma autónoma, poniendo en práctica los conceptos asociados que le habrán sido explicados en clase y comprobando si sus cálculos son correctos.
PyromathsIntroducciónSiguiendo con las herramientas de software libre de ayuda y soporte TIC para la docencia de Matemáticas, vamos a estudiar ahora una aplicación muy sencilla que permite preparar hojas de ejercicios y exámenes. Esta herramienta se llama Pyromaths. Fue creada por Jerome Ortais y es un programa escrito en Python que genera ejercicios o exámenes y su corrección correspondiente. Hay que resaltar que la corrección proporcionada no es sólo la solución final sino que es muy completa, indicando todos los pasos intermedios. En consecuencia puede ser utilizado tanto por los profesores como por los alumnos, ya que tienen disponible la solución detallada de cada ejercicio. La página web del proyecto es http://www.pyromaths.org/. Pyromaths: característicasLa última versión disponible es la 10.06-1. La figura siguiente muestra los créditos donde podemos observar la versión, las personas que han contribuido en el proyecto junto con el autor y que se trata de software libre con licencia GPL.
Existen versiones para Windows y Mac OS, aunque nosotros vamos a trabajar con la versión para GNU/Linux y mas concretamente con el paquete Debian para Ubuntu. Las principales características de Pyromaths son:
Instalación y configuraciónInstalación La instalación la realizaremos mediante el paquete .deb específico. La aplicación no está disponible directamente en los repositorios de Ubuntu. Por tanto hemos de crear un archivo sources.list específico para Pyromaths. La siguiente orden ejecutada desde una terminal genera el archivo /etc/apt/sources.list.d/pyromaths.sources.list e incluye como contenido la línea deb correspondiente:
Comprobamos que se ha generado el archivo indicado:
Comprobamos el contenido del archivo:
Importamos las claves gpg del repositorio incluido:
Actualizamos la lista de paquetes disponibles incluyendo ya el nuevo repositorio:
Instalamos Pyromaths:
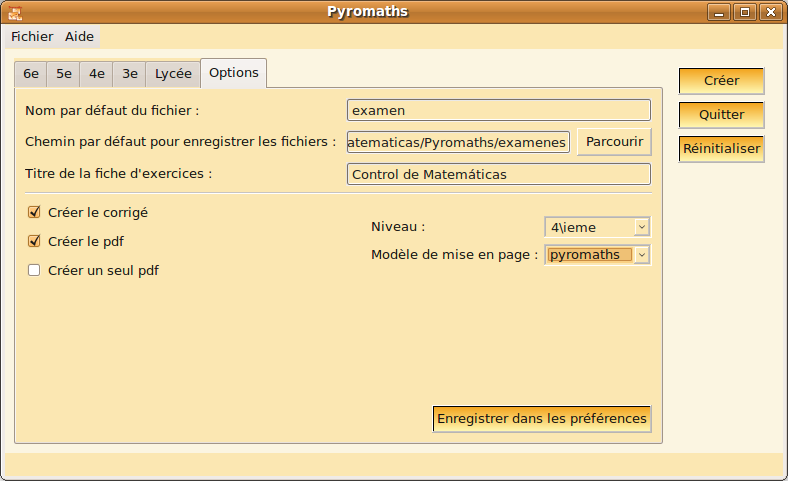
Esta instalación incluye todas las dependencias del paquete, como es el caso de PyQt4 y LaTeX. Una vez instalado el programa está disponible en Aplicaciones > Educación > Pyromaths. Configuración (Options) La configuración que permite Pyromaths es mínima. Para ello ir a la pestaña Options en la interfaz que muestra. Nos deja establecer:
Cada vez que se hagan modificaciones sobre las opciones disponibles hay que pulsar el 'Enregistrer dans les préférences' es decir, Guardar las preferencias. El archivo que contiene las preferencias es ~/.config/pyromaths/pyromaths.xml disponible desde el home del usuario.
Utilización de PyromathsLa interfaz que muestra Pyromaths es la siguiente: 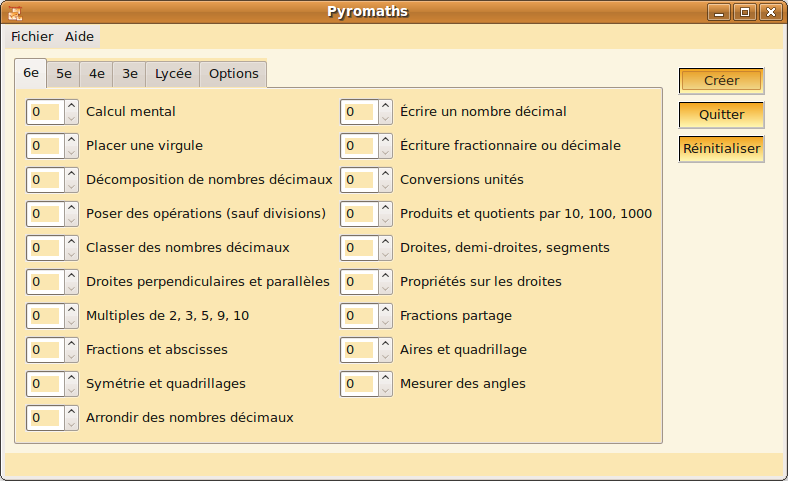 La tabla siguiente muestra la equivalencia entre los sistemas educativos francés y español para poder los niveles en los que se puede utilizar la herramienta. La información se ha obtenido de http://www.mec.es/sgci/fr/es/estudios/equivalencias.shtml
En base a esta tabla cada profesor puede averiguar los contenidos curriculares de sus cursos a qué nivel corresponden en Francia y seleccionar los ejercicios correspondientes. Nosotros, como muestra de su utilización, tomamos como referencia el equivalente a 2º de la ESO que es el nivel 4e francés. Los botones disponibles desde la interfaz son:
Preparación del examen u hoja de ejercicios Simplemente seleccionando el número de ejercicios de cada tipo que se quieren poner en el examen o actividad y pulsando en Créer, es suficiente. El programa pregunta donde almacenar los archivos generados y ya tenemos listo el examen y, en documento aparte, las soluciones. Ejemplo 1 La figura siguiente muestra un posible examen o actividad que consta de 2 ejercicios de cálculo mental. El programa genera un archivo pdf con los enunciados y otro archivo pdf con las soluciones. Además incluye los archivos fuente en LaTeX (.tex) para ambos. 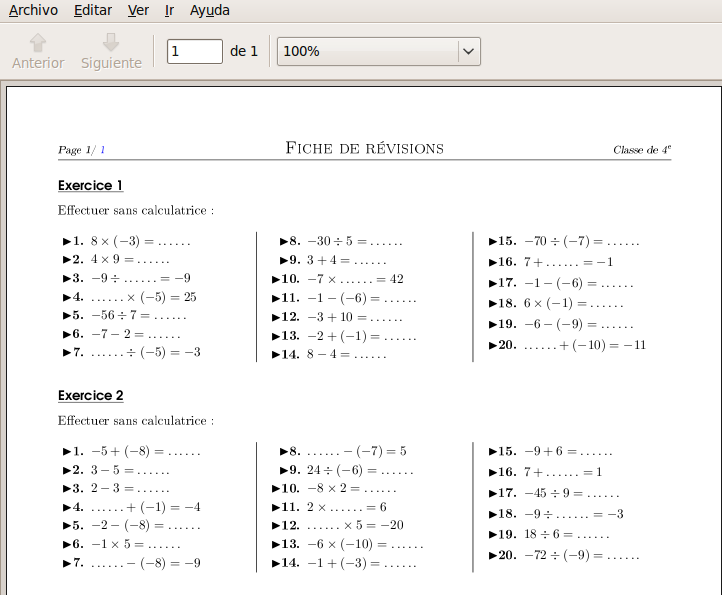 El archivo con las soluciones: 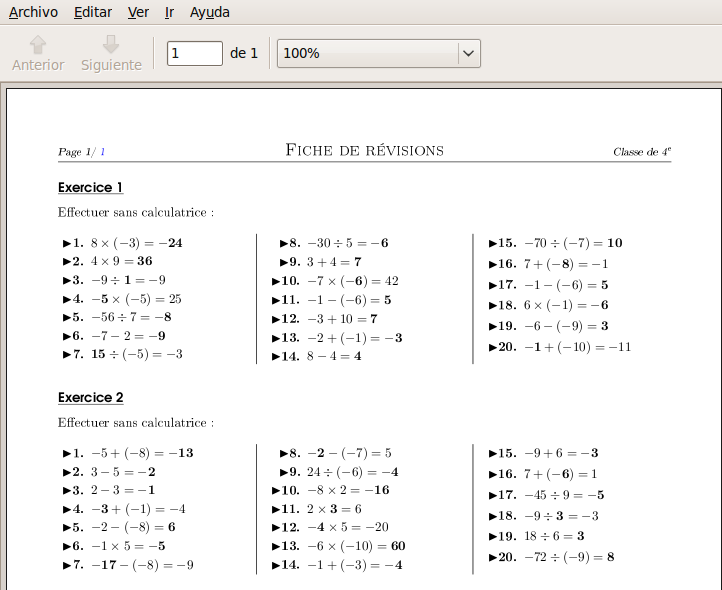 Como se puede comprobar los textos salen en francés. La aplicación no permite seleccionar idioma, pero si que se pueden editar los fuentes y traducir y/o personalizar los enunciados. Ejemplo 2 Si nos planteamos poner un examen mas complicado mezclando ejercicios de diferente tipo, podemos marcar el número de ejercicios de cada apartado que se quiera incluir. Por ejemplo, vamos a poner un examen que contenga 2 ejercicios de cada una de las materias siguientes:
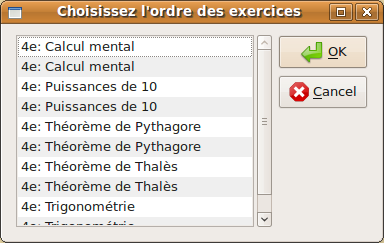
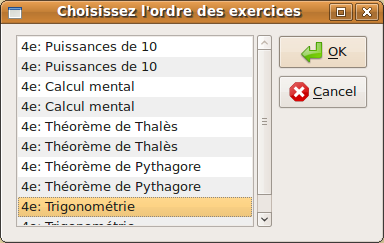
 Cuando se pulsa en Créer ,como hay ejercicios de diferente tipo, el programa da opción a que se modifique su orden de aparición en el archivo generado. Para ello simplemente seleccionar y arrastrar hasta que ocupe el lugar en el orden que queramos y soltar.
Pulsar en OK y se generan en el directorio establecido en Opciones los archivos correspondientes, como en el caso anterior. La figura siguiente muestra el Control de Matemáticas generado.
Cada vez que se genera una hoja de ejercicios y/o exámenes podemos personalizar el título indicando la fecha o la información que consideremos de interés. Dependiendo del tipo de actividad podemos también proporcionar al alumno la hoja de corrección para que pueda él mismo comprobar los fallos que ha tenido y puntuarse. Como podemos observar existe un problema importante, y es que los enunciados están en francés. Pero haciendo uso de los fuentes podemos editarlos y traducirlos para que nuestros alumnos lo entiendan. Es una tarea añadida, pero realmente compensa. Ejemplo 3 Se trata de utilizar la opción Fichier > Tous les exercices. En este caso el programa genera un archivo pdf hoja de ejercicios y un archivo soluciones (con su fuente) para cada uno de los niveles existentes. La nomenclatura es 3e.pdf, 4e.pdf, 5e.pdf,... Viene a ser como un recopilatorio de todos los ejercicios que Pyromaths genera para un año determinado. Es importante tener en cuenta que el proceso lleva su tiempo, ya que se generan para todos los niveles. Personalizaremos los textos desde un editor de LaTeX (que veremos a continuación) y la figura siguiente muestra el aspecto del cuadernillo de ejercicio para 2º de la ESO (4e):
Edición de hojas de ejerciciosExisten gran cantidad de editores de LaTeX dentro del software libre. En concreto para Ubuntu están Lyx y Texmaker, ambos muy conocidos. Podemos instalar, por ejemplo, Texmaker desde Sistema > Administración > Gestor de paquetes Synaptic. Su instalación genera una entrada de menú en Aplicaciones > Oficina . Al ejecutarlo muestra la siguiente interfaz:
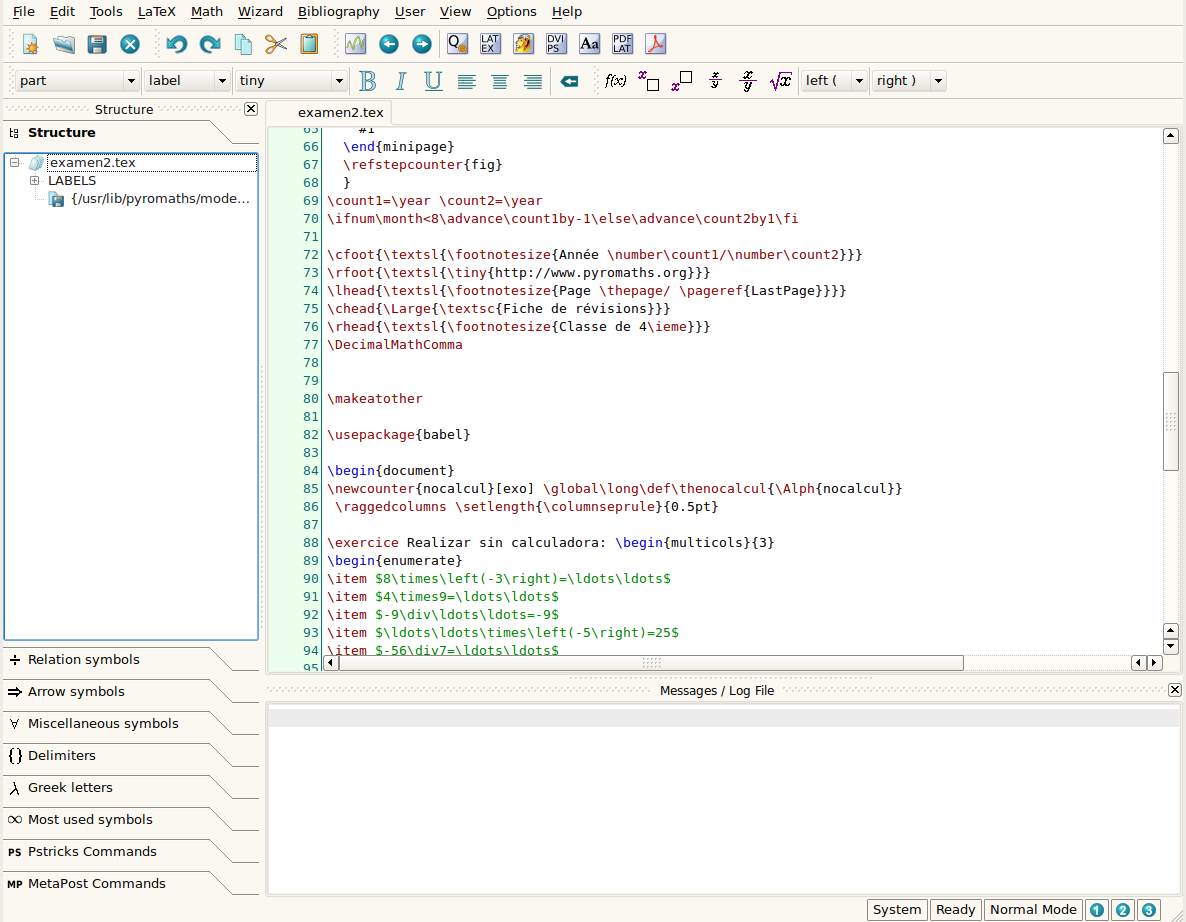
No vamos a hacer una explicación de cómo utilizar este editor ya que nos ocuparía todo un artículo. Si se quiere conocer en profundidad las características y funcionamiento de este editor LaTeX, en la página web del proyecto http://www.xm1math.net/texmaker/index.html hay disponible un manual de usuario que se puede consultar (http://www.xm1math.net/texmaker/doc.html). También hay un manual de usuario en la propia aplicación, en la opción de menú Help. Nuestro objetivo es mucho mas humilde. Simplemente queremos que los textos de los enunciados y todo aquello que se pueda de forma sencilla, poder escribirlos en castellano para que los alumnos lo puedan entender. Abrimos, por ejemplo, la hoja de ejercicios que hemos generado en el Ejemplo 1.
Texmaker muestra lo siguiente:
Como se puede observar hemos modificado el texto 'Realizar sin calculadora'. Es entretenido, pero podemos buscar los textos en francés y traducirlos al castellano. Si ahora pulsamos el botón PDFLAT se actualiza el archivo .tex y se genera el archivo PDF correspondiente en el mismo directorio. Si pulsamos el botón Visor PDF veremos el aspecto del documento modificado:  ConclusiónComo vemos Pyromaths puede ser muy útil en el aula. El profesor de matemáticas puede, en pocos minutos, preparar tarea para los alumnos y puede facilitarles las soluciones para que ellos los revisen. El problema es que la interfaz y los documentos generados están en francés. Esperemos que alguna distribución GNU/Linux se tome interés por ella y la traduzca al castellano. |