Enunciado
Una persona de 60 kg de masa desciende sobre una plataforma de madera de 25 kg con forma de cuña, resbalando por un plano inclinado 30º respecto a la horizontal tal como se indica en la figura. Suponiendo que no existe rozamiento entre la madera de la cuña y el plano, calcular:

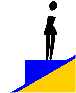
a) La aceleración con que desciende la cuña al iniciarse el movimiento.
b) La Fuerza de inercia sobre la persona
b) El peso aparente de la persona (fuerza con la que cuña lo empuja hacia arriba).
c) La aceleración de bajada si existe un coeficiente de rozamiento entre la cuña y el plano de valor 0,2.

Resolución del problema 3
Memorización de datos y adecuación al S.I.

Aplicando la 2ª Ley de Newton, SF = m·a, en los ejes x e y (ver figura).

Una componente del peso de la plataforma -cuña y de N´empujan la plataforma contra el plano y generan la fuerza de reacción de este igual a N. Si las proyectamos en el eje y vemos que sus efectos se contrarrestan y el sistema no se mueve en el eje y.

N - (P_c· cos 30º+ N´cos 30º) = 0

En el eje x si que existe movimiento:
La componente P_c· sen 30º + N´sen 30º (descomposición según el eje x) comunica a la masa de la plataforma una aceleración, a (aceleración de la plataforma paralela al plano):

P_c· sen 30º + N´sen 30º = m· a

Considerando ahora que le ocurre a la persona vemos que:
La plataforma empuja a la persona hacia arriba con N´que es la misma fuerza con la que la persona empuja a la plataforma (una fuerza menor a su peso = P_p)

La fuerza peso de la persona menos N´, le comunica una aceleración vertical igual a aquella con la que la persona baja unida a la plataforma = a·sen30º (esta es la componente de la aceleración con la que desciende paralela al plano) Pp - N´= mp·a·sen 30º N´ = Pp- mp·a·sen 30º

Usando las dos fórmulas obtenidas anteriormente:

P_c· sen 30º + N´sen 30º = m_c· a
N´=P_p- m_p· a· sen 30º

Tenemos:
25 ·9,8·0,5 + N´·0,5 = 25·a
N´= 60·9,8 - 60·a ·0,86

Resolviendo el sistema de ecuaciones:
25 ·9,8· 0,5 + (60· 9,8- 60· a· 0,5)·0,5 = 25·a
122,5 + 294 - 15 a = 25. a
a = 10,41m·s^-2 (en la dirección paralela al plano y hacia abajo)

La mujer se mueve hacia abajo sometida a una aceleración vertical menor que si cayera en caída libre: a = g = 9,8 m·s^-2
a · sen 30º = 5,2 m·s^-2
aceleración vertical 5,2 m·s^-2

b) Ojo. Debido a la forma de la cuña la fuerza normal sobre la persona, N´, tiene una dirección diferente a la ejercida sobre la cuña por el plano, N.
La fuerza de inercia tiene como valor el producto de la masa por la aceleración y sentido contrario a la aceleración del sistema en que se sitúa la persona.

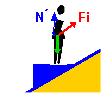
Fi = - m·a = 60 · 10,41 = 624,6 N

La dirección de esa fuerza de inercia es paralela al plano y hacia atrás.
Sobre la mujer actúa una componente del peso que la impulsa hacia abajo, pero como aparece una fuerza de inercia por estar acelerada sobre la plataforma, la fuerza de inercia la impulsa hacia arriba y hacia atrás.
Si no se sujeta a algo unido a la plataforma, la componente horizontal la impulsará horizontalmente hacia la derecha (atrás). La persona cae de la plataforma si no se sujeta.

c) El peso aparente de la persona es la fuerza con la que se apoya sobre la plataforma (o aquella con la que la plataformas la empuja hacia arriba, N´). Como la fuerza de inercia tiene una componente que tira en la dirección de la normal, la persona no carga todo su peso sobre la plataforma. (Peso aparente = Peso - Fi sen a).

c-1
Si estudiamos lo que ocurre desde el sistema no inercial (S.R. no I = acelerado) incluiremos la Fi.

En la dirección vertical

N´+ Fi· sen30º - mg = 0
Peso aparente = m_p· g - Fi· sen30º
Peso aparente = 60 · 9,8 - 624,6 · 0,5 = 275,7 N

En la dirección horizontal se requiere una fuerza externa para que la persona no sea acelerada hacia atrás: debe sujetarse
F externa = m·a· cos 30º

c-2
Si lo estudiamos desde el punto de vista de un sistema en reposo (fuera de la plataforma móvil) no detectaremos la fuerza de inercia y haremos el razonamiento expuesto en el apartado a de este problema:SF = m·a, donde vemos que existen unas fuerzas peso y una reacción de la plataforma cuyo efecto sobre la persona es comunicarle una aceleración vertical, a · sen 30º.
N`es el peso aparente y vale:
P_p - N´ = m_p· a · sen 30º
N´= P_p- m_p· a · sen 30º

N´ = 60 · 9,8 - 60 · 10,41· 0,5 0275,7 N
N´ = 275,7 N

Obtenemos el mismo valor desde los dos enfoques (c-1 y c-2) como no podía ser de otra manera.

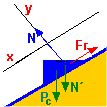
d) Si m = 0,2 la F_r = m· N . La F_r es paralela al plano y se opone al movimiento. Se supone rebasada la Fr máx y que existe movimiento.
Haciendo los mismos razonamientos del apartado a incluyendo Fr tenemos que en el eje y no hay desplazamiento y la suma de fuerzas es cero.
N - (P_c· cos 30º + N´cos 30º) = 0

En el eje x

Por tanto : F_r = m· N = m·(P_c· cos 30º + N´cos 30º)
F_r = 0,2· (25 ·9,8 · 0,86 + N´0,5)

y analizando como se genera el peso aparente, N´, sobre la persona:
N´ = P_p- m_p· a ·sen 30º = 60 · 9,8 - 60· a · 0,5 = 588- 30 · a

Sustituyendo Fr y N´por su valor en : P_c· sen 30º + N´sen 30º - F_r = m · a

25· 9,8· 0,5 + N´·0,5 - 0,2·(25· 9,8· 0,86 + N´ 0,5) = 25·a
25 · 9,8 · 0,5 + (588 - 30·a) · 0,5 - 0,2· (25· 9,8· 0,86 + (588- 30·a)· 0,5) = 25·a
a = 8,52 m·s^-2

Esta aceleración se puede descomponer en una componente vertical y una horizontal.
La componente horizontal impulsará horizontalmente a la persona hacia atrás y, si no la compensa sujetándose a algo unido a la plataforma, caerá.

volver