Enunciado
Supongamos que un conductor de 75 kg que circula en coche a 140 km/h entra en una situación de choque frontal.
a) Al ver el peligro tarda en reaccionar 0,5s e inicia una frenada que dura 4 s antes de iniciar el contacto. Iniciado el choque, desde que contacta hasta que se detiene totalmente transcurre 0,1s. ¿Cuál será la máxima fuerza que soporta, si la frenada previa redujo su velocidad hasta 72 km/h?
b) Antes de entrar en choque frontal, frena rozando durante 5s contra un talud lateral hasta bajar su velocidad a 36 km/h. Finalmente choca frontalmente tardando 0,1s en detenerse. ¿Cuál es la fuerza máxima que soporta en esta situación?

Recuerda: la Fi mata. ¡No mata la velocidad a la que viajas, mata la aceleración con que te detienes!

Resolución del problema 1
Datos en el S.I.
v =144 km /h = 144000/3600 m/s = 40 m/s

a)Vamos a resolverlo situándonos en el S.R. no Inercial (al final puedes ver el enfoque desde un S.R.I.)

Verás que algunos de los datos del enunciado no intervienen para calcular la fuerza del impacto, pero si lo he puesto es para recordarte lo importante que es estar atento a la carretera en todo momento. Debes contar con un tiempo de reacción bajo frente al peligro, pues este tiempo se va a restar del que tienes para frenar ante de empezar a contactar con el obstáculo.

A 140 km/h = 40 m/s, en 0,5 s que tarda en reaccionar recorre 20 metros. Durante el tiempo de frenada en que pasa de 40 m/s a 20 m/s circulará a una media de 30 m/s y recorrerá en los 4 segundos, 30·4 =120m. Para que todo esto sea posible, y puedas disponer de 4,5 s antes del impacto con el objeto, debes estar al menos a 140 m del obstáculo cuando empiezas a reaccionar.

¡Ojo con el tiempo de reacción, se resta siempre al que queda para la frenada!

La velocidad inicial es 40 m/s y la velocidad final = 0.
La velocidad final de frenada es 20 m/s
Aceleración de frenada = Dv / Dt = (20 - 40) /4 = - 5 m·s^-2

Fi = -m·a (Fi opuesta a la aceleración de frenada) durante la frenada.
Fi = -m·a = 75· 5 = - 375 N (ejerce una fuerza contra el volante doble de su peso).

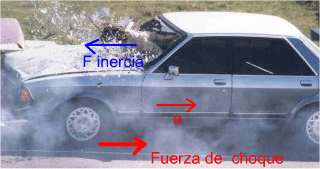
Durante el impacto
La velocidad pasó de 20 m/s a 0.
Aceleración = Dv / Dt = (0 - 20) / 0,1= 200 m·s^-2
Fi = - m·a = -75 · 200 = - 15000 N (20 veces su peso)

Un impacto frontal a 72 Km/h hace que se proyecte con una fuerza de 20 veces su peso hacia el volante (20·9,8 aprox 200). ¿Podrán aguantarla sus brazos? ?¿Y el volante? ¿Soportará esa fuerza el cinturón de seguridad? ¿Podrán los soportes del coche soportarlo o se incrustarán en su cuerpo?

b) Mientras frena contra el talud pasa de 40 m/s a 10 m/s en 5 s y desarrolla una aceleración de frenada de
Aceleración 1 = Dv / Dt = 10 - 40 / 5 = - 6 m·s^-2
la Fi durante esta etapa es baja por ser sólo 6 m·s^-2 la aceleración ya que el rozamiento con el talud duró mucho tiempo.

La aceleración durante el impacto será:
Aceleración 2 = Dv / Dt = 0 -10 / 0,1 =100 m·s^-2
Fi = -m·a = - 75 ·100 = - 7500 N (10 veces su peso)
En este caso al rebajar la velocidad de impacto redujo en un 50% la fuerza del impacto.

Este posible impacto del cuerpo contra el salpicadero lo reducen el cinturón, al frenar el avance hacia delante, y el airbag por ser blando y aumentar el tiempo que tarda en detenerse totalmente.
Durante el impacto, y hasta que no se detiene totalmente, el conductor sale proyectado hacia delante, en sentido contrario a la aceleración de frenada.

Enfoque desde un S.R.I.
Un observador quieto en la carretera no tiene que recurrir a Fi para explicar lo que ocurre. Para él sólo intervienen fuerzas reales que surgen de las interacciones. Para parar el coche y todo lo que va dentro de él cuando marcha a una velocidad, sólo hay que comunicarle una fuerza de frenada (de rozamiento de los neumáticos, del talud o del impacto con el objeto), que la disminuya en los tiempos indicados F = m·D V/ Dt =m·a.
Los resultados obtenidos con este enfoque son los mismos.

volver