| Enunciado
Una persona de 60 kg de masa desciende sobre una plataforma de
madera de 25 kg con forma de cuña, resbalando por un plano inclinado
30º respecto a la horizontal tal como se indica en la figura. Suponiendo
que no existe rozamiento entre la madera de la cuña y el plano, calcular:
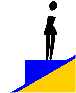
a) La aceleración con que desciende la cuña al iniciarse
el movimiento.
b) La Fuerza de inercia sobre la persona
b) El peso aparente de la persona (fuerza con la que
cuña lo empuja hacia arriba).
c) La aceleración de bajada si existiera un coeficiente
de rozamiento entre la cuña y el plano de valor 0,2.
.Ayuda a la resolución del problema 5
Memorización de datos y adecuación al S.I.
Coloca en una tabla los datos que tienes (en el
S.I) y deja un ? para los que te piden.
| Conocemos |
|
Queremos conocer |
Tabla de soluciones |
| Masa de la persona = mp |
60 kg |
Aceleración. |
? |
| Masa de la plataforma = mc |
25 kg |
Fi |
? |
| Inclinación del plano |
30º |
|
? |
Observa que puedes enfocar el problema desde el punto de un observador
situado en el exterior o de uno situado en la plataforma (en un S.R.
móvil).
Haz un diagrama de fuerzas considerando las que actúan por separado
en la plataforma y en la persona y presta atención a las direcciones
de las mismas: el peso perpendicular al suelo, N perpendicular al plano
y P·sen a paralelo al plano.
Sobre la persona la normal tiene otra dirección (mira la animación).
La resultante de las fuerzas que actúan sobre la cuña en el sentido
del desplazamiento produce una aceleración: SF
= M ·a
En el caso de la existencia de Fi (sólo detectable en S no I.) tiene
una componente que disminuye el peso con el que la persona se apoya
en la cuña y otra componente que la arrastra horizontalmente hacia la
derecha. ¿Se caerá la persona?
¿Debe sujetarse para crear una aceleración hacia la derecha?
Observa la animación y escribe la ecuaciones.
Recuerda que Fr = m ·N
volver
|

