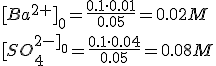Actividad 4.4

Comprueba lo que sabes

Actividad 4.4

Pregunta Verdadero-Falso

Cuando se mezclan 10 ml de BaCl₂ 0.1 M con 40 ml de Na₂SO₄ 0.1 M, precipita sulfato de bario.

El Ks (BaSO4)= 1.1·10⁻¹⁰, indica si es verdadera o falsa la siguiente afirmación:

Después de precipitar el sulfato de bario, las concentraciones de los iones presentes en la disolución serán:

[Ba²⁺] = 18.3·10^-10 M

[Na⁺] = 0.16 M
[SO₄^2-] = 0.06 M

[Cl⁻] = 0.04 M

Verdadeiro Falso

El BaCl₂(s) es soluble:

BaCl₂(s)	→	Ba²⁺(ac)	+	2 Cl⁻(ac)
		0.1 M		0.2 M

El Na₂SO₄(s) es soluble:

Na₂SO₄(s)	→	2 Na⁺(ac)	+	SO₄^2-(ac)
		0.2 M		0.1 M

Para que precipite BaSO₄(s) se deberá cumplir:

[Ba²⁺]₀·[SO₄^2-]₀ ≥ 1.1·10^-10

Como ahora el volumen es de 50 ml (debido a la unión de los dos volúmenes)

Como 0.02·0.08 > 1.1·10^-10, precipitará BaSO4

Para saber cuanto sulfato de bario precipita podemos plantear el equilibrio:

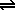
	BaSO₄(s)	Ba²⁺(ac)	+	SO₄^2-(ac)
Inicial		0.02		0.08
Equilibrio		0.02 - x		0.08 - x

1.1·10^-10 = (0.02-x) (0.08-x)

Al ser Ks muy pequeño prácticamente todo el BaSO₄(s) que pueda formarse precipitará, la [Ba²⁺] y la [SO₄^2-] son muy pequeñas y la ecuación de 2ºgrado dará soluciones poco satisfactorias.
Un modo mejor de resolver el problema consiste en:

1. Suponer que precipita todo el BaSO₄(s) posible (como si la precipitación fuera completa).
2. Parte del BaSO₄(s) se disuelve hasta alcanzar el equilibrio de solubilidad:

	BaSO₄(s)	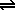Ba²⁺(ac)	+	SO₄^2-(ac)
1. Inicial		0.02		0.08
Final		≈ 0		0.06

2. Inicial		0		0.06
Equilibrio		x		0.06 + x

1,1·10^-10 = x (0.06+x) ≈ x·0,06

x = 18.3·10⁻¹⁰ M

En definitiva: [Ba²⁺] = 18.3·10^-10 M

[Na⁺] = 0.16 M
[SO₄^2-] = 0.06+x ≈ 0,06 M

[Cl⁻] = 0.04 M

Y el número de moles de BaSO₄(s) que precipitan =(0.02-x)·0.05 ≈ 0.001 moles

Licenciado baixo a Creative Commons Attribution-NonCommercial 2.5 License