Ondas
| Cuestiones y Ejercicios. Ondas |

![]()
![]()
7.lc Indicar si es verdadero (V) o falso (F) lo que se afirma:
7.2c Indicar si es verdadero (V) o falso (F) lo que se afirma:
7.3c Un vibrador produce ondas en la superficie de un estanque a intervalos regulares de tiempo. Si se ajusta el vibrador de modo que produzca un número doble de ondas por segundo, en este caso las ondas:
A se propagan con doble velocidad,
B se propagan con la mitad de la velocidad,
C tienen longitud de onda doble,
D tienen la mitad de longitud de onda.
7.4c Un vibrador produce una onda en la superficie del agua cada 0,5 s. Dichas ondas tienen de longitud de onda 3 cm y su velocidad en cm/s es:
A) 1,5 B) 4,5 C) 3,0 D) 6,0
7.5c Indicar la afirmación que es incorrecta:
A las ondas sonoras, en los gases, son longitudinales,
B las ondas longitudinales no se polarizan,
C las ondas sonoras en los líquidos son transversales,
D el movimiento de la partícula es perpendicular a la dirección de propagación de la onda transversal.
7.6c Una cuerda vibra con una frecuencia de f Hz. Si se observa a través de un disco estroboscópico que tiene 4 ranuras igualmente espaciadas, el número mínimo de vueltas por segundo que debe de tener el disco para que la cuerda parezca estacionada es:
A) f B) f/4 C) 2f D) f/2
7.7c El sonido se propaga a través de un gas a 340 ms-1 a la temperatura de l6ºC. Cuando la temperatura es de 127ºC, la velocidad vale:
A) 250 ms-1 B) 55l ms-1 C) 400 ms-1 D) 1700 ms-1
7.8c Dos ondas se propagan en sentido opuesto por una cuerda, con amplitudes de 3 y 2 cm, respectivamente. Cuando se encuentran, la amplitud resultante, en un instante dado es, en cm: |
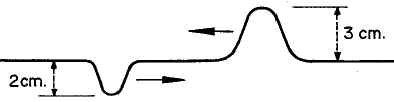 |
A) 1 B) cero C) 5 D) 3
7.9c Una onda luminosa de frecuencia f tiene una longitud de onda l en el aire. Si dicha onda penetra en el agua con una velocidad v, su frecuencia es:
A) l / v B) c/v D) f
7.10c Cuando la luz pasa del aire a través de un vidrio, cambian algunas de estas propiedades:
1) la frecuencia 2) la longitud de onda 3) la velocidad 4) la energía del fotón
7.11c Indicar los fenómenos que se pueden demostrar por medio de la luz invisible:
1) difracción 2) doble refracción 3) interferencias 4) formación de ondas estacionarias
7.12c La ecuación de una onda unidimensional sinusoidal que se propaga por un resorte en sentido positivo es
y(x, t) = Asen (w t - kx) :
7.13c Explicar brevemente la diferencia entre la luz roja emitída por un tubo de gas neón y por una lámpara piloto de un coche.
7.14c El principio de superposición afirma que las elongaciones de dos ondas que interfieren en un punto es igual al vector suma de las elongaciones de las dos ondas; y lo cumplen:
a) las ondas longitudinales b) las ondas transversales c) las ondas electromagnéticas d) las ondas mecánicas
7. 15c El sonido de un violín que oímos en un concierto es una
| a) onda mecánica longitudinal estacionaria, | c) onda mecánica longitudinal progresiva, |
| b) onda transversal electromagnética progresiva, | d) onda mecánica transversal estacionaría. |
7.16c Dos ondas que poseen igual amplitud y frecuencia dan origen a una onda estacionaria, si interfieren:
| a) perpendicularmente | c) con igual velocidad pero de sentido opuesto |
| b) con diferente longitud de onda | d) con diferente frecuencia angular. |
7.17c La ecuación y(x, t) = Asen (w t – kx + j ) representa:
7.18c Dos ondas de la misma amplitud y período interfieren en un punto. La onda resultante se caracteriza porque tiene:
7.19c Representar en un diagrama dos ondas transversales:
7.20c Hallar la onda resultante y dibujarla en los casos a) y e) de la cuestión anterior.
7.21c Si se duplica la amplitud de un movimiento ondulatorio ¿cómo varía la energía?, ¿cómo varía su intensidad?
7.22c El sonido que emite un diapasón es muy débil y se oye sólo a muy corta distancia; pero si se fija a una caja resonante, se oye en toda la clase. ¿Se debe esto a un aumento de energía del sistema?
![]()
Problemas
7.1p La ecuación de una onda transversal sinusoidal unidimensional es:
y (x, t) = 10·sen2p (2,00 t - 0,01 x) medidos x e y en cm y t en segundos. Determinar:
7.2p Una onda periódica se propaga por una cuerda tensa de ecuación:
y (x, t) = 0,4·sen2p (50t - 0,20x) en unidades SI. Calcular:
7.3p Un movimiento ondulatorio se propaga en sentido positivo con velocidad v=30 ms-1, siendo su amplitud 0,1 m y la frecuencia, f = 50 Hz. Determinar :
7.4p En una cuerda elástica se mueve una onda progresiva transversal sinusoidal de ecuación y(x,t)= A·sen(w t + kx ). Determinar su ecuación conociendo las elongaciones en el instante t =0 y la elongación del origen que ocupa la posición x = 0 , en función del tiempo.
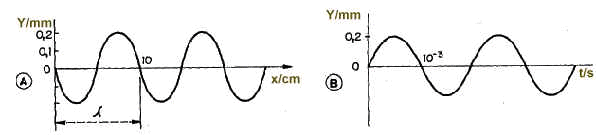
7.5p Una onda se propaga en sentido positivo y suponemos que es sinusoidal, de período T =10 s y amplitud 1,2 m. Determinar:
a) La elongación en el origen en el instante t=1 s.
b) La longitud de onda l , si para t = 1 s la elongación es nula en el punto que dista x =6 cm del origen.
7.6p Una onda sonora plana que se supone sinusoidal se propaga sin amortiguamento en la dirección OX con velocidad v = 350 m/s. La amplitud de la oscilación es A = 3·10-5 m su frecuencia, f = 12 kHz. Si la elongación en el instante inicial en el punto (0,0,0) es 1,5 ·10-5 m hallar:
7.7p Por una cuerda de 15 m de longitud y 0,2 kg de masa se desplaza una onda transversal con velocidad v = 75 ms-1. Se alarga 5 cm la cuerda si se le aplica una tensión doble que la inicial. Determinar:
7.8p Un movimiento ondulatorio unidimensional armónico tiene por ecuación:
y(x,t) = 0,002sen(60x+300t) en unidades SI. Determinar:
7.9p Una onda se propaga por un medio isotrópico con la velocidad de 90 m/s y frecuencia 60 Hz. Se pide:
a) la distancia que hay entre dos puntos A y B si sus elongaciones en un instante dado tienen un desfase de 30º;
b) el desfasamiento que se origina en el punto A entre dos desplazamientos separados en el tiempo t = 0,02s.
7.10p Un movimiento ondulatorio se propaga por un medio elástico según y = 4·sen (2p / t+ j ) en unidades SI. Calcular:
7.11p La ecuación de una onda que se propaga en una dirección es:
y (x, t) = 2·cos 2p (t/0,01-x/30) en unidades SI. Se pide:
|
Cuestionario de opción múltiple
|
|