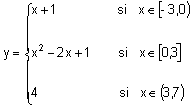|
FUNCIONS DEFINIDES MITJANÇANT OPERACIONS O TRANSFORMACIONS D'ALTRES |
|
2.1. Funcions definides a trossos: Exercici resolt 1 |
||
|
Ara anem a
estudiar amb deteniment com es construeix la gràfica d'una funció
definida a trossos.
Sigui la següent funció:
Primer tros En aquest tros
l'expressió analítica és y = x + 1, una funció lineal, i està definida
per als valors de x que són majors o igual que -3 i menors que 0. Com
és una funció lineal, amb un parell de punts és suficient per a
construir la gràfica. Quan x = -2 => y = -2 + 1 = -1; i quan x =
-1 => y = -1 + 1 = 0. És a dir, la funció passa pels punts (-2,
-1) i (-1, 0). I observa que si agafes un punt x molt proper a x= 0,
aleshores la funció hauria de valer 0, és a dir, pots dibuixar una punt
buit (0, 1)
Ara, en el teu quadern, representa en uns eixos de coordenades aquests dos punts i dibuixa amb traç suau una línia recta que passi per aquests punts.
Segon tros En
aquest tros la fórmula de la funció és y = x2 -
2x + 1, en l'interval
[0, 3] i la seva representació gràfica és una paràbola d'eix vertical.
Com el coeficient de x2 és positiu, la paràbola
és còncava. Ara determinarem diversos punts de la parábola i els
unirem.
El vèrtex té per abscissa x = 1: per a x = 1=> y = 12 - 2·1 + 1 = 0. El vèrtex (1, 0) es troba en l'interval on aquesta funció està definida. Calculem uns quants punts més, per a x = 0 => y = 02 - 2·0 + 1 = 1; per a x = 2 => y = 22 - 2·2 + 1 = 1 i per a x = 3 => y = 32 - 2·3 + 1 = 4 Les coordenades dels punts són (0, 1), V(1, 0), (2, 1) i (3, 4). Representa aquest quatre punts en el teu quadern i uneix-los amb traç suau.
Tercer tros En aquest tros
la funció és y = 4 i està definida quan x pertany a l'interval (3, 7).
La gràfica de la funció és una recta horitzontal i per a dibuixar-la
has de dibuixar un segment horitzontal entre x = 3 i x = 7 a alçada y =
4. Els extrems del segment són punts buits.
Igual que has fet a l'apartat anterior, dibuixa amb traç suau aquest segment. Observaràs que el punt (3, 4) del tros anterior "enganxa" amb el punt buit (3, 4) d'aquest tros. Finalment dibuixa amb traç fort cadascun dels trossos de la funció. |
||
|
En aquesta
escena tens la gràfica de la funció que has dibuixat en el teu quadern.
Compara ambdues gràfiques.
Pots veure els valors de les coordenades dels diferents punts de la funció arrossegant el control gràfic P.
|
||
| Luis Caballero Tejero, traducció i adaptació a càrrec de Zoila Pena Terrén, febrer 2009 |
 |
© Ministerio de Educación , Política Social y Deporte. Año 2006. |