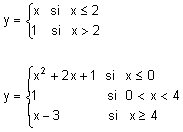|
FUNCIONS DEFINIDES MITJANÇANT OPERACIONS O TRANSFORMACIONS D'ALTRES |
|
2. Funcions definides a trossos |
||
|
Les següents
funcions tenen unes expressions analítiques molt especials.
Aquestes
funcions requereixen diverses fórmules, cadascuna de les quals regeix
el comportament de la funció en un cert tram o "tros".
Representar aquestes funcions és fàcil si saps representar cadascun dels trossos i poses atenció al comportament de la funció en els punts de ruptura (punts en els quals es passa d'un tros a un altre). La primera funció val y = x (primer tros) quan x és menor o igual que 2, i y = 1 (segon tros) quan x és major que 2. Els punts de ruptura són els valors de x en els quals la funció passa d'un tros a un altre. En aquests punts la funció pot estar definida en un tros o en l'altre, o fins i tot prendre un valor diferent al que pogués correspondre-li en cadascun dels trossos o fins i tot no estar definida. En aquest primer exemple, el punt de ruptura està en x = 2 i la funció està definida en el primer tros. Quan en el punt de ruptura la funció presenta una discontinuïtat, en aquest cas de salt, es representa l'extrem del tros en el qual està definida la funció amb un cercle ple o amb color i en el tros en el qual no està definida amb un cercle sense emplenar o colorejar. |
||
|
En aquesta
escena tens la gràfica de la primera de les funcions anteriors. Observa
com es comporta la funció en les proximitats del punt de ruptura.
Pots arrossegar el control gràfic P i anar veient els valors que pren la funció, en el tros en el qual està definida i l'expressió analítica d'aquest tros.
|
||
|
Si desitges
veure la gràfica de la segona funció i treballar amb ella, només has
de canviar el control numèric f de 1 a 2. Observa que aquesta funció no
presenta cap discontinuïtat en els punts de ruptura, ja que la funció
en aquests punts pren el mateix valor en un tros o en un altre.
|
||