| 1. Multiplica vectores por números |
- La flecha designada por u es un vector
- El vector 2u tiene la misma dirección y el mismo sentido que u y es doble de largo, o sea su módulo es el doble.
- Análogamente se forman los vectores
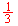 u y -3u (éste
está dirigido en sentido contrario a u) u y -3u (éste
está dirigido en sentido contrario a u)

- El vector u avanza 3 y sube 1. Por eso lo designamos así: u (3,1). Al par (3,1) se le llama componentes del vector u
- Análogamente
- 2u = (6,2). Es
decir, 2u = 2(3,1) = (6,2)
- -3u = (-9,3) retrocede 9 y baja 3
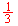 u = (1, u = (1,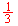 ) )
|
|
EJERCICIO
1
Observa la figura que viene a continuación.
Cambia los valores del número o escalar a, y verás como cambia el
módulo del vector au.
| Si alguna vez se
te sale algún vector de la pantalla, puedes mover los ejes pulsando en OX
o en OY, o cambiar el zoom. |
| Para cambiar los
valores de a puedes pulsar los botones adjuntos a él o teclear el valor
que quieras y pulsar Enter. |
|
|
|
Ayudándote de esta figura
y de los cambios que les puedes introducir, escribe en tu cuaderno las respuestas a las
siguientes cuestiones: a) Si a=1,
¿cómo son los módulos de los vectores u y au?
b) Si a=2, ¿cómo son las direcciones de los vectores u
y au?
c) Si a=-3, ¿cómo son los sentidos de los vectores u
y au? |
| EJERCICIO 2 Cambiando los valores de m, n y p podrás ir
obteniendo los vectores ma, nb, y pc.
Naturalmente
- si m=1,
ma=1.a=a
- si n=1,
nb=1.b=b y
- si p=1,
pc=1.c=c
|
|
|
a) Teniendo a la vista los vectores a, b y c, escribe
en tu cuaderno las componentes de cada uno de estos vectores.
b) Representa en esta figura el vector 3c, y
mirando el vector resultante, escribe en tu cuaderno sus componentes.
c) Compara las componentes del vector c con las
del vector 3c. ¿Qué operación se ha efectuado? |
d) Repite los apartados b) y
c) para los vectores a y -2a
e)Idem para 1.5b
f)Encuentra el número, tal que podamos expresar el vector d como producto de uno de los vectores a, b o c por ese número. Escribe en tu cuaderno el valor
de dicho número. |
| CONCLUSIONES |
| Un vector AB queda determinado por dos
puntos, origen A y extremo
B que es donde se encuentra la punta de la flecha. |
 |
| Módulo
de un vector a es la longitud del vector y
se expresa con la misma letra entre barras. Módulo del
vector a = |a| |
| Dirección
del vector es la dirección de la recta donde se encuentra y la de todas sus paralelas.
Por ejemplo los vectores x e y tienen la misma dirección. |
 |
| El sentido
de un vector lo indica la punta de la flecha. Por ejemplo los vectores x e y
tienen el mismo sentido. |
| Dos vectores son iguales si tienen el mismo módulo, la misma
dirección y el mismo sentido. |
| Dos vectores iguales x e y
situados en rectas distintas determinan un paralelogramo. |
|
|
Compruébalo en esta escena,
trasladando el vector y horizontal o/y
verticalmente.
Puedes comprobar que son iguales haciendo
que se superpongan. También puedes comprobar que se pueden poner en la misma recta, o sea
que tienen la misma dirección. |
El producto 0v es igual al vector
cero, 0. Es un vector cuyo origen y extremo coinciden y, por tanto, su
módulo es cero. Carece de dirección.
El vector -1v
se escribe -v y se llama opuesto de v. |
|
EJERCICIO 3 (RESUMEN)
En esta escena puedes mover con el ratón los puntos B y D, de tal manera que el vector u
tiene la dirección constante y sólo puedes variar su módulo, y el
vector v tiene el módulo constante y sólo puedes
variar su dirección y sentido.
Compruébalo moviendo B y D.
Pulsa inicio y no hagas ningún movimiento hasta que se te indique.
Escribe en tu cuaderno ayudándote de la escena: |
|
|
a) Origen
del vector u
b) Extremo del vector v
c) Componentes de u y v
d) Módulo de los vectores u y v (ayúdate del teorema de Pitágoras)
e) Mueve el punto D con el ratón, de tal manera que los vectores u y v
tengan la misma dirección y sentido contrario |
f) Tal como
quedó la figura en el apartado anterior, escribe el vector v como producto
de un número por el vector u
g) Mueve el punto B, para que quede u=v
h) Con la figura del apartado anterior, dibuja en tu cuaderno el paralelogramo
que forman los vectores u y v
i) Mueve el punto B para que el vector u se nos
convierta en el vector cero. Copia en tu cuaderno como te ha quedado la
figura. |


