
 |
MATRICES: INVERSA DE UNA MATRIZ |
| Álgebra | |
| 11. INVERSA DE UNA MATRIZ |
|
Dada una matriz cuadrada A, si existe otra matriz B del mismo orden que verifique: A . B = B . A = I ( I = matriz identidad ), se dice que B es la matriz inversa de A y se representa por A-1. Si existe la matriz inversa de A, se dice que la matriz A es inversible o regular. En caso contrario, se dice que la matriz A es singular. ¿Cuándo tiene inversa una matriz? Una matriz A de orden n (n filas y n columnas) tiene inversa cuando su rango es n, es decir, cuando el rango de dicha matriz coincide con su orden. ¿Cómo se puede calcular la inversa de una matriz? Básicamente hay tres procedimientos para calcular la inversa de una matriz. Son los siguientes: 1º Aplicando la definición y resolviendo los sistemas de ecuaciones correspondientes. Resulta muy laborioso cuando el orden de la matriz es superior a 2. 2º Por el método de Gauss. 3º Por determinantes y adjuntos (que describiremos en la unidad de determinantes). En esta unidad nos centraremos principalmente en el método de Gauss. |
| 12. CALCULO DE LA INVERSA DE UNA MATRIZ APLICANDO LA DEFINICIÓN | |
|
La siguiente escena describe como se calcula la inversa de una matriz de orden 2 o de orden 3 aplicando la definición. |
|
|
Este procedimiento es bastante laborioso y poco recomendable cuando el orden de la matriz es mayor que 2, pues, por ejemplo, para una matriz de orden 3 hay que resolver 3 sistemas de ecuaciones lineales, cada uno de ellos con tres ecuaciones y tres incógnitas. |
|
| 13. CALCULO DE LA INVERSA DE UNA MATRIZ POR EL MÉTODO DE GAUSS | |
|
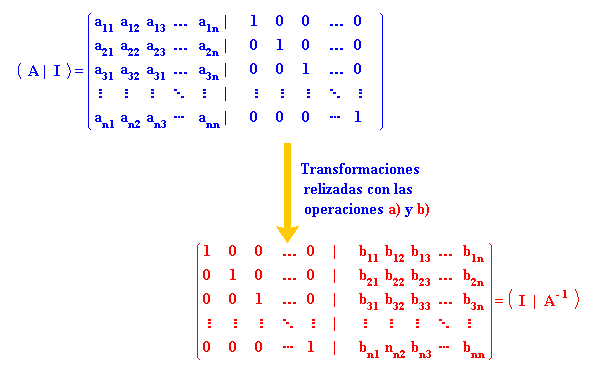
Para calcular la inversa de una matriz cuadrada A, aplicando el método de Gauss, construimos, en primer lugar, la matriz ( A | I ), siendo I la matriz identidad del mismo orden que A. Después de realizar diversas operaciones sobre las filas de ésta nueva matriz, tendremos que conseguir que se transforme en la siguiente ( I | B ). La matriz B será la inversa de la matriz A, es decir: B = A-1. Las operaciones que podemos realizar con las filas de la citada matriz son: a) Multiplicar o dividir una fila por un número distinto de cero. b) Sumarle a una fila otra fila multiplicada por un número distinto de cero. |
|
 |
En las escena inferior izquierda se describe el proceso, paso a paso mediante un ejemplo, para calcular la inversa de una matriz de orden 3 aplicando el método de Gauss. Al pulsar sobre los botones de la parte inferior derecha se abren sendas escenas que permiten calcular la inversa de cualquier matriz de orden 2 o 3 por el método de Gauss, también con una descripción de los pasos realizados. |
|
|
| Alfredo Pena Iglesias | ||
 |
||
| © Ministerio de Educación, Política Social y Deporte. Año 2006 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.