SIMETRÍAS: NIVEL BÁSICO
Geometría
 
1. SIMETRÍA AXIAL
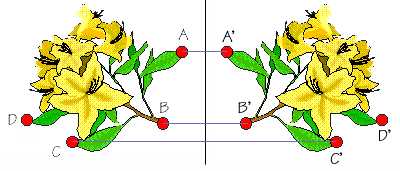
simetria.jpg (15362 bytes)En la figura siguiente se muestra un ejemplo de simetría axial. En este caso el eje de simetría es una recta vertical. Las rectas AA', BB', CC' y DD' son ahora perpendiculares al eje de simetría y la distancia desde A al eje coincide con la distancia del punto transformado A' al eje. En definitiva, para obtener el transformado de un punto, en una simetría axial, hay que trazar la perpendicular al eje de simetría que pasa por el punto y situar el punto A', sobre esta perpendicular, a la misma distancia del eje que A.

Definición: Se llama simetría axial de eje r, a un movimiento que transforma un punto A en otro A1 de modo que r es mediatriz del segmento AA1, o lo que es lo mismo, d(A, r) = d(A1, r).

En la siguiente escena puedes mover los puntos A, B y C con un eje concreto. Para cambiar el eje puedes mover los parámetros m (pendiente del eje) y n (ordenada del eje en el origen).
 
Actividad para experimentar y observar 1.- Mueve los puntos A, B y C,  observa como se comportan los puntos A1, B1, C1 y los segmentos A1B1 y B1C1.
   
Actividad para escribir en las HOJAS DE TRABAJO 2.- Cambia los parámetros m (pendiente del eje) y n (ordenada del eje en el origen) y explica que sucede.
   
Actividad para escribir en las HOJAS DE TRABAJO 3.- ¿Hay algún punto doble en una simetría axial?
2. SIMETRÍA AXIAL RESPECTO AL EJE X
Cuando se consideran unos ejes coordenados hay ciertas rectas que tienen gran importancia, vamos a ir considerando a esas rectas ejes de simetrías. En la siguiente escena tenemos una simetría axila respecto al eje x, es decir, respecto de la recta y=0.
 

 
Actividad para escribir en las HOJAS DE TRABAJO 4. Busca cuál es el punto simétrico del punto A, (mueve el punto A1 a esa posición). ¿Qué se puede afirmar de los simétricos con respecto al eje OX?
2. SIMETRÍA AXIAL RESPECTO AL EJE Y
Cuando se consideran unos ejes coordenados hay ciertas rectas que tienen gran importancia, vamos a ir considerando a esas rectas ejes de simetrías. En la siguiente escena tenemos una simetría axila respecto al eje x, es decir, respecto de la recta x=0.
 

 
Actividad para escribir en las HOJAS DE TRABAJO 5. Busca cuál es el punto simétrico del punto A, (mueve el punto A1 a esa posición). ¿Qué se puede afirmar de los simétricos con respecto al eje OY?
 
3. SIMETRÍA AXIAL RESPECTO AL OTRAS RECTAS
Cuando se consideran unos ejes coordenados hay ciertas rectas que tienen gran importancia, vamos a ir considerando a esas rectas ejes de simetrías. En la siguiente escena tenemos una simetría axila respecto al eje x, es decir, respecto de la recta y=x.
 

 
Actividad para escribir en las HOJAS DE TRABAJO 6. Busca cuál es el punto simétrico del punto A, (mueve el punto A1 a esa posición). ¿Qué se puede afirmar de los simétricos con respecto al eje de simetría  y=x?
 
Cuando se consideran unos ejes coordenados hay ciertas rectas que tienen gran importancia, vamos a ir considerando a esas rectas ejes de simetrías. En la siguiente escena tenemos una simetría axila respecto al eje x, es decir, respecto de la recta y=-x.
 
Actividad para escribir en las HOJAS DE TRABAJO 7. Busca cuál es el punto simétrico del punto A, (mueve el punto A1 a esa posición). ¿Qué se puede afirmar de los simétricos con respecto al eje de simetría  y=-x?
 
       
           
Joaquín Comas Roqueta
 
© Ministerio de Educación y Ciencia. Año 2007