| Recta de Regresión de Y sobre X |
|
| Recta de Regresión de X sobre Y |
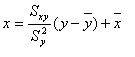 |
| ESTADÍSTICA |
| Tema 2: Distribuciones Estadísticas Bidimensionales |
| RECTAS DE REGRESIÓN. ESTIMACIÓN |
La condición de que la suma de los cuadrados de las diferencias verticales (yi - yr )2 podría sustituirse por la de la suma de los cuadrados de las diferencias horizontales ( xi - xr )2 . En este caso obtendríamos la recta de regresión de X sobre Y. Es decir, en realidad hay dos rectas de regresión, la de Y sobre X, que es la que hemos calculado y la de X sobre Y. Intercambiando los papeles de X e Y obtenemos las dos ecuaciones
| Recta de Regresión de Y sobre X |
|
| Recta de Regresión de X sobre Y |
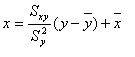 |
| En la siguiente escena puedes plantear gráficamente distintos diagramas de dispersión. Aparecen doce puntos que puedes mover libremente por toda la escena con el ratón. En color verde se representa la recta de regresión de Y sobre X. En color morado, la recta de regresión de X sobre Y. El valor de r es el coeficiente de correlación lineal de Pearson. El punto azul tiene por coordenadas las medias de las dos variables. |
|
|
| ACTIVIDADES |
|
Actividad 1. En la posición en la que aparecen los puntos, el coeficiente de correlación lineal de Pearson tiene un valor muy próximo a 0. Intenta conseguir el valor 0 para r. ¿Qué sucede con las rectas de regresión? |
|
Actividad 2. a) Coloca los puntos en una línea recta que no sea ni horizontal ni vertical. ¿Qué sucede con el coeficiente de correlación? ¿Qué sucede con las rectas de regresión? b) ¿Qué sucede con las rectas de regresión cuándo se aproxima r a 1? c) ¿Qué sucede con las rectas de regresión cuándo se aproxima r a -1? d) ¿Qué sucede con las rectas de regresión cuándo se aproxima r a 0? e) Coloca ahora los puntos en una línea recta vertical u horizontal, ¿que sucede con las rectas de regresión? ¿Cómo es la correlación entre las variables? Intenta explicar lo que está sucediendo en esa situación.
|
|
Actividad 3. a) Coloca los puntos intentando construir una parábola. ¿Cómo son las rectas de regresión? Explica esta situación. b) Coloca ahora los puntos en dos líneas perpendiculares que se cruzan (por ejemplo paralelas a las bisectrices de los cuadrantes y que tenga seis puntos cada línea) ¿Cómo son ahora las rectas de regresión? ¿Es lógica esta situación? ¿Por qué? c) Construye otros diagramas de dispersión que se te ocurran y observa las rectas de regresión. |
|
Actividad 4 a) ¿En qué punto se cortan siempre las dos rectas de regresión? b) ¿Cómo es el comportamiento de las rectas en el sentido de creciente o decreciente? c) Si el ángulo que forman las dos rectas es muy pequeño, la correlación es ¿fuerte o débil? ¿y si el ángulo es cercano a los 90º? |
|
Estimaciones. Una vez que conocemos la mayor o menor relación entre las variables con el coeficiente de correlación lineal y que hemos calculado las rectas de regresión, podemos utilizarlas para predecir el valor de una de las variables a partir de la otra. Por ejemplo, en el ejemplo de la distancia a canasta y número de encestes, tenemos datos para una distancia de 6 metros y de 7 metros, ¿pero qué pasará si el jugador tira desde 6.5 metros? ¿o incluso, si vuelve a hacer los lanzamientos desde 6 metros, cuántas encestará? Igual sucede con lo de los pesos y las estaturas, ¿cuánto es previsible que pese una persona de esa población que mida 179 cm? ¿O cuánto debe pesar una persona que mide 1.70 m? Pues utilizando la recta de regresión pertinente, podemos responder a esto sustituyendo y haciendo cálculos. En algo similar a esto se basan las máquinas de las farmacias. Después de haberlo calculado, nos podemos preguntar si este dato obtenido es fiable o no. Esto dependerá de dos cuestiones: La primera que exista correlación lineal entre ambas variables. El dato será más fiable cuanto más se aproxime el coeficiente de correlación lineal a 1 o a -1, y si queremos afinar más, ya sabes, el coeficiente de determinación. La segunda que las rectas de regresión se han obtenido para unos valores concretos de X y de Y. Aunque exista una correlación lineal fuerte, si intentamos hacer predicciones para valores de las variables lejanos a los estudiados, podemos llevarnos sorpresas. Es decir, para que sea fiable una estimación, además de la primera condición, los valores de X e Y tienen que estar dentro del dominio de los estudiados.
|
||||||||||||
|
Veamos un ejemplo: Un resorte se alarga cuando en el extremo se coloca un peso. La longitud del resorte en cm y el peso en g colgado viene dado por la tabla:
¿Qué longitud se supone qué tendrá el resorte al colgarle un peso de 6 g? ¿ Y de 28 g? ¿Son fiables ambas estimaciones?
|
||||||||||||
| Puesto que nos están preguntando por una longitud sabido un peso, tendremos
que calcular la recta de regresión de la longitud respecto al peso , esto es, la
recta de regresión de Y sobre X. Haciendo todo el cálculo estadístico de
medias, desviaciones, y covarianza, obtenemos que: Por tanto, si colocamos un peso de 6 g → y = 3,18 · 6 +13,74 = 32.82 → alargamiento esperado es 32.82 cm. Igualmente para x = 28 g sustituimos y nos sale que y = 102.78 cm. Para responder a la fiabilidad de las predicciones miramos al coeficiente de correlación lineal. Puesto que r = 0.996, podemos decir que la primera predicción es muy fiable, si queremos afinar más, calculamos R2 = 0.9962 = 0.992 → fiable en un 99.2%. La segunda predicción es muchísimo menos fiable, pues aunque el coeficiente de correlación es el mismo, el dato de 28 g se escapa completamente de los datos obtenidos en la tabla, por tanto no podemos asegurar que sea fiable. Si por ejemplo nos hubiesen preguntado que qué peso habrá que colocar para producir un alargamiento de 35 cm, tendríamos que haber calculado la otra recta de regresión, la del peso sobre el alargamiento, es decir, la de X sobre Y. Ojo: aquí no valdría sustituir la "y" por 35 cm y despejar la "x", pues la recta de regresión no es una función exacta que establezca relaciones entre las dos variables, sino que establece "estimaciones."
|
 |
|
|
|