VECTORES FIJOS  
Geometría
 
       
1. Dos Puntos en el Plano
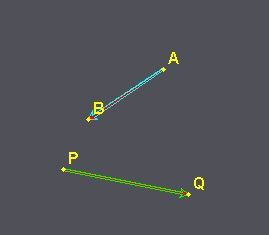
En el plano, dos puntos cualesquiera determinan un segmento, como el representado en la escena de color verde.

Si al segmento le añadimos una punta de flecha, le damos un sentido, tendremos un vector, como el de color rojo.

Tanto el segmento como el vector, tiene una longitud que podemos medir, a esto llamamos modulo. También están sobre la recta que determinan los puntos extremos, a esto le llamamos dirección.

Lo que no tiene el segmento, es lo que indica el Afijo, que es el sentido.

En el plano cada dos puntos determinan un vector, a cada uno de ellos se le llama Vector Fijo
2. Vectores Equipolentes
-Si tenemos dos vectores, puede ocurrir que tengan la misma longitud (Modulo) que tengan la misma Dirección, y que tengan el mismo Sentido (el afijo señala hacia el mismo sitio)

-Con el Ratón mueve uno de los punto A o C, se cambian de posición los vectores AB o CD.

-¿Como son estos vectores obtenidos respecto de los iniciales?.

-Utiliza el control Azul, haz que Dibuja tenga el valor 1. ¿Que tipo figura se obtiene?

-Cambia de posición uno de los vectores ¿Cual es la característica de todos los cuadriláteros obtenidos?

 

Anota en tu cuaderno tus conclusiones.
-Regla del Paralelogramo, si al unir los puntos extremos de dos vectores  AB CD no alineados, el polígono obtenido es un paralelogramo. Los vectores AB CD tienen igual Modulo (longitud), tienen la misma dirección (paralelos), y los afijos indican que tienen el mismo Sentido.
- Dos Vectores que verifiquen la Regla del Paralelogramo, se dice que son equipolentes.
 

-Los vectores  AB o CD, están sobre la misma recta. Ahora no podemos construir un paralelogramo para compararlos. ¿Que tendremos que hacer?.

-Utiliza el control Azul, haz que Dibuja tenga el valor 1.

-Utiliza el control Azul, haz que Dibuja tenga el valor 2.

-Utiliza el control Azul, haz que Dibuja tenga el valor 3.

 

Anota en tu cuaderno tus conclusiones.

- Si tenemos dos Vectores Alineados, si encontramos otro Vector que es Equipolente a los primeros, entonces estos son Equipolentes
       
           
  Jaime S. Herrero de Evan
 
Ministerio de Educación, Cultura y Deporte. Año 2004
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.