logo RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
Geometría
 
1. Datos necesarios para resolver un triángulo rectángulo

Además del ángulo recto necesitamos dos datos:
  • Hipotenusa (a) y un ángulo (C ó B).
  • Hipotenusa (a) y un cateto (b ó c).
  • Dos catetos (b y c).
  • Un cateto (b ó c) y un ángulo (C ó B)  .

Las fórmulas que relacionan los lados y los ángulos son las siguientes:

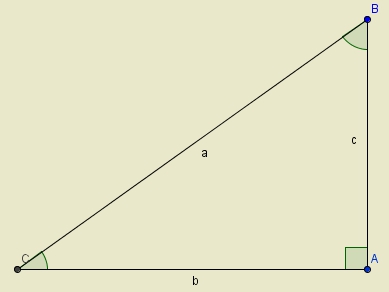rectangulo

Relación de lados: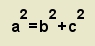

forlado

Relación de ángulos: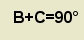

angulo

Relación de lados con ángulos:

forangulo


En la siguientes aplicaciones de Descartes puedes comprobar las relaciones existentes entre los lados y los ángulos en un triángulo rectángulo.
Caso 1: Conocidos los lados a y b o el lado a o b y un angulo B o C
Esta unidad interactiva requiere la máquina virtual de Java J2RE.
En el applet de la izquierda  puedes crear un triángulo rectángulo conocida la longitud de los lados a y b. Puedes variar la longitud de estos lados con los controles de la parte inferior y ver como van variando todos los parámetros que definen al triángulo. En la parte de arriba con el comando zoom puedes alejar o acercar la escena a conveniencia y con O.x y O.y puedes desplazar la posición del triángulo para una mejor visión del mismo. 

1.- Resolver un triángulo rectángulo en el que b es igual a 15 m. y B=69º .

2.- Resolver un triángulo rectángulo, sabiendo que a=30 m. y b=23 m. 
Caso 2. Conocidos los lados a y c o el lado a o c y un angulo B o C
Esta unidad interactiva requiere la máquina virtual de Java J2RE.
En el applet de la izquierda  puedes crear un triángulo rectángulo conocida la longitud de los lados a y c. Puedes variar la longitud de estos lados con los controles de la parte inferior y ver como van variando todos los parámetros que definen al triángulo. En la parte de arriba con el comando zoom puedes alejar o acercar la escena a conveniencia y con O.x y O.y puedes desplazar la posición del triángulo para una mejor visión del mismo. 

3.- Resolver un triángulo rectángulo en el que a=10 metros y B=27.30º .
Caso 3. Conocidos los lados b y c
Esta unidad interactiva requiere la máquina virtual de Java J2RE.
En el applet de la izquierda  puedes crear un triángulo rectángulo conocida la longitud de los lados b y c. Puedes variar la longitud de estos lados con los controles de la parte inferior y ver como van variando todos los parámetros que definen al triángulo. En la parte de arriba con el comando zoom puedes alejar o acercar la escena a conveniencia y con O.x y O.y puedes desplazar la posición del triángulo para una mejor visión del mismo. 

4.- Resolver un triángulo rectángulo tal que b=27 m. y c=43 m. 
Resolución de triángulos isósceles
Esta unidad interactiva requiere la máquina virtual de Java J2RE.
En el applet de la izquierda  puedes crear un triángulo isósceles conocida la base b y la altura h . Puedes variar estas variables con los controles de la parte inferior y ver como van variando todos los parámetros que definen al triángulo. Con el comando Trazarh puedes trazar la altura y ver como el triángulo isósceles se puede descomponer en dos triángulos rectángulos lo que permite resolverlo aplicando las propiedades expuestas más arriba. En la parte de arriba con el comando zoom puedes alejar o acercar la escena a conveniencia y con O.x y O.y puedes desplazar la posición del triángulo para una mejor visión del mismo. 

5.-La base de un triángulo isósceles mide 24 cm y la altura 28 cm. Resolverlo.
 
 
       
  Manuel Durán Vacas
logo2  
Ministerio de Educación, Cultura y Deporte. Año 2011
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.