
 |
RESOLUCIÓN DE TRIÁNGULOS DE CUALQUIER TIPO |
| Geometría | |
| 1. Resolución de triángulos de cualquier tipo. | ||
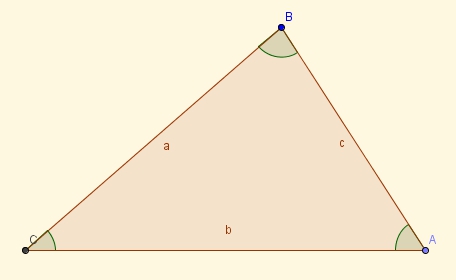 |
Se nos presentan cuatro casos, según que los datos seán:
Siempre nos deben dar un lado, al menos, como dato. En la práctica, mejor que distinguir estos casos será saber relacionar las incógnitas con los datos que nos dan. Necesitamos dos teoremas (el de los senos y el del coseno) para poder resolverlos. |
|
| Manuel Durán Vacas | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2011 | ||

Los
contenidos de esta unidad didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.