TÉCNICAS DE RECUENTO

3.2.- Variaciones con repetición

Variaciones con repetición de m elementos tomados de n en n son los distintos grupos que se pueden formar con los m elementos, de manera que:

• En cada grupo entren n elementos repetidos o no.
• Dos grupos son distintos si difieren en algún elemento o en el orden de colocación.

El número de variaciones con repetición de m elementos tomados de n en n se representa por

3.2.1- Actividades

Resuelve en tu cuaderno de trabajo

7.- En una bolsa hay 8 bolas numeradas del 1 al 8. Sacamos una bola, anotamos su número y la devolvemos a la bolsa.¿Cuántos resultados distintos se pueden dar?

Comprueba tus resultados en la escena

4.- Combinaciones sin repetición

Combinaciones ordinarias o sin repetición de m elementos tomados de n en n ( n<=m ) son los grupos que se pueden formar con los m elementos, de manera que:

• En cada grupo entren n elementos distintos.
• Dos grupos son distintos si difieren en algún elemento.

En este caso no importa el orden a la hora de formar los grupos.

El número de combinaciones ordinarias de m elementos tomados de n en n se representa por Cm,n .

Usando factoriales:

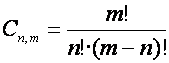
Ejemplo

En una clase de 25 alumnos se quiere formar un equipo de baloncesto con 5 de ellos. ¿De cuántas formas diferentes se puede elegir el equipo?

4.1- Actividades

Resuelve en tu cuaderno de trabajo los siguientes ejercicios:

8.- Una heladería tiene helados de 12 sabores. ¿Cuántos cucuruchos de 2 sabores diferntes puede hacer? ¿Y de 3 ?

9.- En una familia de 6 personas se acuerda que cada día se encarguen dos personas de las tareas domésticas. ¿ Cuántos grupos se pueden formar?

Comprueba tus resultados en la escena

Inicio

Blasa Pérez Hernández   Ministerio de Educación, Cultura y Deporte. Año 2005

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.