

TÉCNICAS DE RECUENTO
1.- Diagrama en árbol. Principio general de recuento
Si un primer experimento puede hacerse de m formas diferentes y un segundo experimento puede hacerse de n formas diferentes, entonces los dos experimentos juntos pueden hacerse de m · n formas diferentes.
Ejemplo
Una chica tiene en su armario 5 camisetas, 6 pantalones de deporte y 3 pares de zapatillas.¿De cuántas formas diferentes podrá vestirse para hacer deporte?
Observa el siguiente diagrama y extrae tus propias conclusiones
1.1- Actividades
Resuelve en tu cuaderno de trabajo los siguientes ejercicios:
1.- En la carta de un restaurante el cliente puede elegir su menú, escogiendo un primer plato, un segundo plato y el postre.La carta tiene 8 primeros platos, 10 segundos y 15 postres. ¿ Cuántos menús diferentes puede elegir cada cliente?
2.- Para financiar el viaje de fin de curso, un grupo de alumnos ha encargado unas camisetas en dos colores: blanco y azul. Si las tallas son pequeña, mediana, grande y extragrande, ¿cuántos modelos diferentes de camisetas tendrán que elaborar?
Comprueba tus resultados en la escena
2.- Permutaciones
2.1- Permutaciones sin repetición. Factorial
Permutaciones ordinarias de n elementos son los distintos grupos que se pueden formar de manera que:
El número de permutaciones ordinarias de n elementos se representa por Pn y vale:
Pn = n(n-1)(n-2)···3 · 2 · 1
A este número se le llama factorial de n y se representa por n! siendo n un número natural o nulo.
Ejemplo
¿ De cuántas formas diferentes pueden sentarse 5 personas en una fila de butacas?
P5 = 5 ! = 5 · 4 · 3 · 2 · 1 = 120
2.1.1- Actividades
Resuelve en tu cuaderno de trabajo los siguientes ejercicios:
3.- En un campeonato comarcal hay tres equipos: Baza, Caniles y Freila, que se disputan los tres primeros puestos. ¿Cuántas clasificaciones se pueden obtener?
4.- El coro del instituto está formado por 19 alumnos. ¿De cuántas formas diferentes se pueden colocar teniendo en cuenta que el solista siempre está en el centro?
Comprueba tus resultados en la escena
2.2.- Permutaciones con repetición
Una colección de n objetos, clasificados en k grupos de objetos idénticos entre sí, el primero con n1 objetos, el segundo con n2, ...se pueden ordenar de
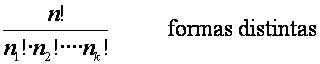
Ejemplo
Con los símbolos a, a, a, b, b, c, c, d ¿cuántas palabras se pueden formar de 8 letras?
Puesto que hay que usar todos los símbolos
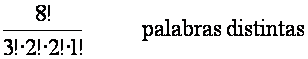
3.- Variaciones
3.1.- Variaciones sin repetición
Variaciones ordinarias o sin repetición de m elementos tomados de n en n (n <= m) son los distintos grupos que se pueden formar con los m elementos, de manera que:
El número de variaciones ordinarias de m elementos tomados de n en n se representa por Vm,n y es igual a:
Vm,n = m(m-1)(m-2)...(m-n+1)
Utilizando factoriales se pueden expresar:
Vm,n = m!/ (m-n)!
Ejemplo
En una carrera participan 5 corredores. Suponiendo que no pueden llegar dos al mismo tiempo, ¿de cuántas maneras se pueden repartir los 3 primeros puestos?
Para ocupar el primer puesto hay 5 corredores, para el segundo 4 y para el tercero 3. Por tanto hay 5 · 4 · 3 formas diferentes de ocupar los tres primeros puestos. Coincide con V5,3 = 5 ·(5-1)·(5-3+1) = 5 · 4 · 3
3.1.1- Actividades
Resuelve en tu cuaderno de trabajo los siguientes ejercicios:
5.- ¿ Cuántos números de 3 cifras se pueden formar con los dígitos 1, 2, 3, 4, 5, 6, 7, 8 y 9 sin que se repita ninguna cifra?
6.- En un I.E.S. hay 35 profesores, ¿de cuántas formas diferentes se puede elegir el equipo directivo formado por director, jefe de estudios y secretario?
Comprueba tus resultados en la escena
|
|||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.