NÚMEROS COMPLEJOS
FORMA BINÓMICA
1. INTRODUCCIÓN
Necesidad de ampliar los números reales
Al resolver algunas ecuaciones de segundo grado con coeficientes reales como la siguiente, se obtienen raíces que no son números reales porque hay que hallar la raíz cuadrada de un número negativo. Para resolver estas ecuaciones se necesita ampliar el conjunto de los números reales.
Ejemplo:
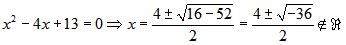
La unidad imaginaria
La unidad imaginaria es
y se representa por
(
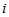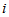viene
de imaginario)
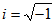
Utilizando esta definición de unidad imaginaria ya se pueden hallar las raíces cuadradas de los números negativos.
Conjunto de los números complejos
A partir de los números reales se define el conjunto de los números complejos de la siguiente forma:
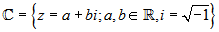
Forma binómica de un número complejo
La forma binómica de un número complejo es la expresión a+bi, a se llama la parte real y b la parte imaginaria.
Si la parte imaginaria es nula, entonces el número es real. Por tanto, los números reales están contenidos en los números complejos.
Se llaman números imaginarios puros a los que tienen parte real igual a cero.
Representación gráfica de los números complejos
Los números complejos se representan en unos ejes coordenados en el plano, que se llama plano de Gauss. La parte real se representa en el eje de abcisas X, que se llama eje real y la parte imaginaria en el eje de ordenadas Y, que se llama eje imaginario.
El afijo de un número complejo es el punto que se le hace corresponder en el plano. El afijo del número complejo z=a+bi es el punto P(a,b).
1.- Mueve el punto en los cuatro cuadrantes del plano y comprueba la relación entre los números complejos y las coordenadas de los afijos.
2. OPERACIONES EN FORMA BINÓMICA
Suma y resta de números complejos
Para sumar o restar números complejos en forma binómica se suman o se restan las partes reales y las partes imaginarias.
2a.-
Comprobar gráficamente que la suma de los segmentos correspondientes a las
partes reales e imaginarias de 
y
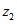son los segmentos correspondientes a las
partes real e imaginara de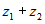 
.
Multiplicación de números complejos
Para multiplicar números
complejos en forma binómica se multiplican como binomios teniendo en cuenta que
.
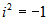Ejemplo
Sea z1=2+3i y z2=4+5i entonces z1+z2=(2+3i)·(4+5i)=8+10i+12i+15i2=8+22i-15=-7+22i
2b.-Comprobar que en forma binómica que hay ninguna relación gráfica sencilla entre las partes real e imaginaria de z1, z2 y su producto.
Conjugado de un número complejo
El conjugado de un número
complejo de obtiene al cambiar el signo de la parte imginaria y se representa
por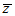 
.
División de números complejos
Para dividir dos números complejos en forma binómica se multiplica el numerador y el denominador por el conjugado del denominador.
Ir a la segunda parte del tema
| |||||||||||||||
