|
Para la
resolución de los siguientes ejercicios puedes ayudarte de la
calculadora matricial, situada al final de esta página.
También
puedes comprobar la solución, pulsando sobre el botón correspondiente de
cada ejercicio.
-
Las calificaciones
de matemáticas, de cuatro alumnos de 2º de Bachillerato, en las tres
evaluaciones del curso fueron las siguientes:
|
|
CALIFICACIONES |
|
Alumnos |
1ª Ev |
2ª
Ev |
3ª Ev |
|
Antonio |
8 |
7 |
5 |
|
Jaime |
4 |
6 |
5 |
|
Roberto |
6 |
5 |
4 |
|
Santiago |
7 |
6 |
8 |
Para calcular
la calificación final, el departamento de matemáticas ha
establecido los siguientes "pesos" para cada una de las
evaluaciones: 1ª Ev: 25 %, 2ª Ev: 35 % y
3ª Ev: 40 %. Se pide:
a) La nota
final de cada uno de los alumnos.
b) La media
aritmética de las calificaciones de cada evaluación.
-
Tres familias
numerosas van a una heladería. La primera familia pidió 3 helados de
barquillo, un helado de vasito y 2 granizadas, la
segunda familia consumió 1 helado de barquillo, 4 helados de vasito y
una granizada y la tercera familia, 3 helados de barquillo, 2 helados
de vasito y 2 granizadas.
a) Obtén una
matriz A, 3 x 3, que exprese el número de helados de barquillo,
helados de vasito y granizadas que consume cada familia.
b) Si cada una de
las tres familias ha gastado respectivamente: 13 €, 12€
y 15€, calcula el precio de un helado de barquillo, un
helado de vasito y una granizada.
-
Dadas las matrices
A y B, se pide:
a) Calcula, si es
posible, los productos A.B y B.A.
b) Calcula, si es
posible, (A.B) -1.
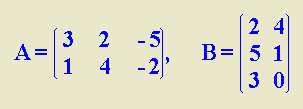
-
Resuelve la
ecuación matricial: A.X.B = C, siendo:

-
Calcula An siendo A:
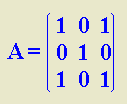
-
Resuelve la ecuación matricial:
A.X - 4.B = X, siendo:
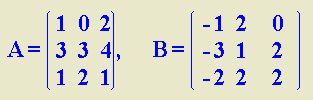
-
Calcula el rango de las siguientes matrices:
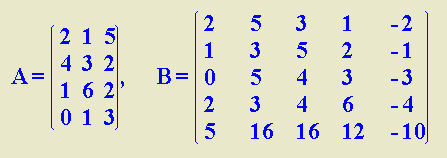
|