D. Rectas tangente y normal a la gáfica

7. Ecuaciones de las rectas tangente y normal a la gráfica de una función derivable

Conociendo de una recta un punto cualquiera A (x₀,y₀) y su pendiente m, la ecuación punto-pendiente es:    y - y₀ = m ( x - x₀ )
Si el punto está en la gráfica de una función entonces es A(a,f(a)).
Ya sabemos que la recta tangente tiene como pendiente la derivada en a, es decir f'(a). Así la ecuación de la recta tangente es:

La recta normal es perpendicular a la anterior, y las rectas perpendiculares tienen pendiente inverso-opuesta, es decir, -1/f'(a). Así la ecuación de la recta normal es:

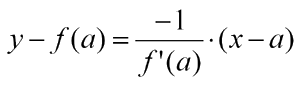
En la siguiente escena aparece la gráfica de una función, un punto de la misma A(a,f(a)), las rectas tangente (en verde) y normal (en morado) y una recta amarilla que puedes editar escribiendo en su ecuación, que aparece en la parte inferior. Observa que en la escena ya aparecen calculadas las pendientes de las dos rectas. Por ahora, deja el control dificultad en 0.

7.37.- Aplicando las ecuaciones punto-pendiente específicas para la recta tangente y normal haz coincidir la recta amarilla editable con cada una de ellas. Para intentarlo en otra situación pulsa el control animar. Puedes terminar cuando consigas dos éxitos consecutivos (en ambas rectas).

Para profundizar:

7.38.- Si cambias el control dificultad a 1, las pendientes de las rectas tangente y normal desaparecen y aparece la expresión de la función. Pulsa animar. Deriva la función y calcula dichas pendientes. Puedes evaluar tu nivel de acierto poniendo de nuevo el nivel de dificultad a 0 con lo que aparecerá el resultado.
7.39.- Pulsa el control animar hasta que la recta tangente sea horizontal ¿Podrías explicar qué sucede en esa situación?

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.