C. Interpretación geométrica de la derivada

5. Tasa de variación media y recta secante a la gráfica de la función.

Dado un incremento de la variable independiente h, la tasa de variación media (TVM) en x=a correspondiente a ese incremento es el cociente entre lo que varía la función f(a+h) -f(a) y la variación de la variable h.

TVM(a,h) = ( f(a+h)-f(a) )  /  h

Ahora que ya estás familiarizado con las gráficas de Descartes, manipula la escena siguiente hasta que identifiques todos los elementos. Básicamente tienes la gráfica de una función y=f(x), un punto de la misma A(a,f(a)), un incremento con respecto de la "a", h, que define un punto B, y la recta que pasa por A y B, que llamaremos recta secante (porque corta a la gráfica en dos puntos).

5.24.- Copia en la hoja de experimentación todos los valores que aparecen en la parte superior, añadiendo una breve descripción de su correspondencia geométrica
5.25.- Calcula la tasa de variación media para los siguientes valores de a y h: (a=1,h=2) (a=1,h=0.5) (a=2, h=-1) (a=2, h=0)
5.26.- ¿Por qué no hay recta secante para h=0? ¿Por qué no existe la TVM para h=0?
5.27.- Habrás observado que los dos datos en verde (TVM y tag(ángulo)) coinciden.¿Por qué?
5.28.- De las escenas anteriores ya sabes que la pendiente de una recta es la tangente del ángulo que forma con OX+. Completa la siguiente frase:

"La Tasa de Variación Media es la _ _ _ _ _ _ _ _ _ de la recta _ _ _ _ _ _ _"

5.29.- Pulsa inicio. Aumenta la escala y sitúate alrededor del punto A(1.8,1.23). Dale valores muy pequeños a "h" (por ejemplo 0.0002, 0.0001). Parece que para valores muy pequeños de "h" el ángulo se estabiliza. ¿En qué valor?

6. Interpretación geométrica de la derivada de una función en un punto

La derivada de una función en un punto es el límite cuando h toma valores próximos a cero de la Tasa de Variación Media en "a" con incremento "h". Es decir:

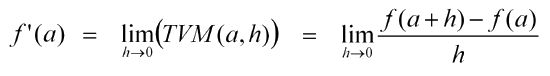
En la escena anterior ya hemos concluido que la tasa de variación media es la pendiente de la recta secante. Ahora tienes dibujada en verde la recta tangente a la gráfica en A(a,f(a)). Se trata ahora de que observes la animación y veas en que recta se transforma la secante para valores de "h" muy próximos a cero.

6.30.- Mueve primero el punto A (con el control de la abscisa "a") y comprueba que la recta verde es la recta tangente a la gráfica en A(a,f(a))
6.31.- Pulsa inicio. Disminuye el valor de "h" hasta que sea cero. ¿Qué pone donde se leía TVM(a,h)? ¿Por qué?
6.32.- Dale a "h" valores próximos a cero. ¿A que valor va tendiendo el ángulo?
6.33.- Pulsa animar. ¿Qué valores toma h? Cuando "h" toma valores próximos a cero ¿con que recta parece coincidir la recta secante?¿a qué valor tiende la TVM?
6.34.- Ya sabemos que la TVM es la pendiente de la recta secante. Piensa en qué se transforma cada uno de los elementos subrayados para valores de "h" próximos a cero y completa la siguiente frase:

"La _ _ _ _ _ _ _ _ de una función en un punto, f'(a) es la pendiente de la recta _ _ _ _ _ _ _ _ _ "

Para profundizar:

6.35.- La función de la escena es f(x)= - sen(x+pi/2) + 1. El punto A es (pi/2,1). Comprueba que f'(pi/2)=1
6.36.- Si la pendiente de la recta tangente es m=1, y el punto es A(pi/2,1) comprueba que la recta tangente tiene de ecuación      y - 1 = 1 * (x - pi/2)

puedes pasar a la siguiente página pulsando la flecha azul hacia la derecha que hay debajo.

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.