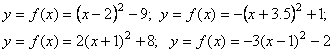
1.-En la siguiente escena aparecen funciones cuadráticas más generales. Haz variar el valor de los parámetros. Utiliza el ZOOM si lo crees necesario.
2.-Escribe en el cuaderno lo que le ocurre a la gráfica según cambien los valores de A, B y C. Observa que para representar la parábola los puntos que más información dan son el vértice y los de corte con los ejes, además del eje de simetría. En caso de que la parábola no corte al eje horizontal, te puede ser de ayuda obtener dos puntos simétricos, a un lado y otro del vértice.
3.-La parábola tiene un extremo relativo. ┐Cuándo es un máximo relativo? ┐Cuándo un mínimo relativo?
4.-Localiza el vértice, los puntos de corte con los ejes y dibuja en el cuaderno la gráfica de las siguientes parábolas.
IV)Expresión general de la parábola.
Si en la expresión
![]()
desarrollas el paréntesis y reagrupas, llegarás a una de la forma
![]()
que es la habitual para las funciones cuadráticas.
Para representar la gráfica lo que debes hacer es encontrar los puntos de ella que más información te den: los puntos de corte con los ejes y el vértice. Trazar el eje de simetría te será de ayuda, especialmente si la parábola no corta al eje horizontal, así como la obtención de un par de puntos simétricos, a un lado y otro del vértice. En la siguiente escena verás algunos ejemplos.
1.-Da distintos valores a los parámetros y observa la gráfica de la función. Aparecen las coordenadas de los puntos de corte con los ejes y el vértice (Utiliza el ZOOM y mueve los ejes si es necesario).
Para encontrar los puntos de corte con el eje horizontal ( y=0 ), y con el eje vertical ( x=0 ) debes resolver los sistemas:
![]()
![]()
Las coordenadas del vértice son:
![]()
2.-Haz en tu cuaderno las operaciones necesarias para representar las parábolas siguientes. Comprueba el resultado introduciéndolas en la escena.
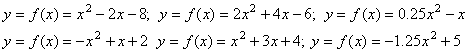

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.
|
|||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.