4.9. Transformaciones de una función: Ejercicios resueltos 2.

En este apartado vas a ver otros dos tipos de ejercicios resueltos sobre transformaciones de funciones.

1. Asocia a cada una de las siguientes gráficas su correspondiente expresión entre las siguientes: 

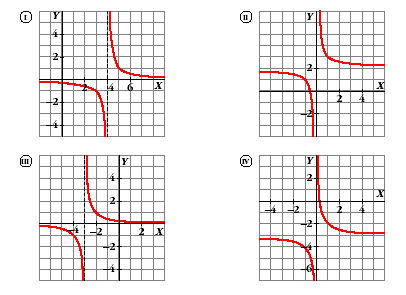
Al  observar  las  expresiones  analíticas  de las funciones, todas se pueden considerar transformaciones de la función y = 1/x . La representación gráfica de esta función son hipérbolas cuyas asíntotas coinciden con los ejes de coordenadas.

a) Aquí la función y = 1/x sufre una traslación vertical de dos unidades hacia arriba, su gráfica se corresponde con la II.

b) La función y = 1/x está sometida a una traslación horizontal de 3 unidades hacia la izquierda y la gráfica resultante se corresponde con la III.

c) En este caso hay una traslación vertical de la función original de tres unidades hacia abajo y la gráfica se corresponde con la IV.

d) La función y = 1/x, en este caso, experimenta una traslación horizontal de 4 unidades hacia la derecha y la gráfica resultante es la I.

2. Utilizando la relación:

Podemos escribir la función:

de la siguiente forma:

Comprueba que su gráfica coincide con la de y =1/x trasladada 1 unidad hacia la izquierda y 2 unidades hacia arriba.

Si hicieras la gráfica de la función comprobarías fácilmente lo anterior. Cuando tengas una función racional cuyo numerador y denominador son funciones polinómicas de primer grado, siempre puedes utilizar la relación anterior y comprobar que su gráfica tiene la misma forma que la de y = 1/x pero trasladada horizontalmente y verticalmente. Puedes utilizar la siguiente escena para ver la gráfica de y = 1/x y su transformada.

En esta escena se muestra la gráfica de la función f(x) = 1/x. 

Si deseas ver la gráfica de la función:

dale al control numérico g el valor 1.

I.E.S. Alcaria. La Puebla del Río (SEVILLA)