CIRCUNFERENCIA
Geometría
 
1. DEFINICIÓN DE CIRCUNFERENCIA. EUACIÓN DE UNA CIRCUNFERENCIA.
La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. La distancia del centro a un punto de la circunferencia se llama radio.
Si de una circunferencia conocemos el centro C(a,b) y el radio, su ecuación será: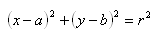        
                                                ecuación circunferencia

La ecuación desarrollada es: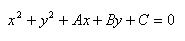                
                                                ecuación

                                 
Esta unidad interactiva requiere la máquina virtual de Java J2RE. 3.- Da diferentes valores a los parámetros A, B y C y observa cómo varía el centro y el radio de la circunferencia. 

4.-Encuentra, en tu cuaderno de trabajo, la relación entra los parámetros A,B, C y las coordenadas del centro y el radio.

5.-Indica cuáles de las siguientes ecuaciones corresponden a circunferencias y, en ellas, identifica el centro y el radio.

                   ecuaciones

Cuando hayas hecho este ejercicio en tu cuaderno de trabajo, comprueba tus soluciones en la escena.

3. DETERMINACIÓN DE UNA CIRCUNFERENCIA
Podemos determinar la circunferencia que pasa por dos puntos A y B, y que tiene su centro en una recta dada. El centro de la circunferencia está en la mediatriz del segmento AB, si además está en una recta dada, basta con resolver el sistema para conocer sus coordenadas.
Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Aumenta el valor del paso y apareceran los elementos que tienes que ir hallando para llegar finalmente a la circunferencia.

6.- Invéntate dos puntos y halla, en tu cuaderno, la ecuación de la circunferencia que pasa por esos dos puntos, y cuyo centro está en la recta dada en la escena. Después, comprueba con esta escena que lo has hecho correctamente.


Para mover los puntos puedes mover las flechas para ir cambiando el valor de sus coordenadas, o también, puedes escribir en las celdillas el valor que les quieras dar y presionar después intro.
Utiliza el cambio de escala cuando lo necesites.
7.-¿Qué ocurre cuando A(2,1) y B(3,2)? ¿Y cuando A(-1,2) y B(0,3)? Cambia, en la escena los valores de A y B por estos otros y observa lo que ocurre. ¿Llegas a alguna conclusión? Si es así, describe, en tu cuaderno estas dos situaciones. Encuentra otros puntos con los que ocurra ésto.
4. DETERMINACIÓN DE UNA CIRCUNFERENCIA II
En general,se necesitan tres puntos o tres condiciones para determinar la ecuación de una circunferencia.
Esta unidad interactiva requiere la máquina virtual de Java J2RE.

8.- Mueve los tres puntos y vete aumentando el valor del paso, la escena mostrará un método para determinar la circunferencia que pasa por esos tres puntos.

Ahora tambien puedes mover el punto seleccionándolo con el ratón y arrastrándolo, o bien pulsando las teclas de flechas.

9.-Escribe en tu cuaderno la ecuación de la circunferencia que pasa por los puntos A(-3,3); B(-2,0) y C(1,3), siguiendo los pasos que aparecen en la escena. Comprueba la solución introduciendo estos puntos en la escena.

10.-¿Qué ocurre cuando los puntos son A(1,0); B(3,-1) y C(-3,2)? Da una condición para que tres puntos determinen una circunferencia. Escribe esta condición en tu cuaderno de trabajo.
    atras   ll  
           
  Irene Valero Matas
 
Ministerio de Educación, Cultura y Deporte. Año 2010
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.