
 |
Conjuntos. Operaciones con conjuntos |
|
Cardinal de un conjunto |
|
|
|
Como ya hemos estudiado antes, los conjuntos finitos son los que tienen “unos pocos” elementos, más concretamente, son tales que podemos contar los elementos que tiene.
El
cardinal de un
conjunto finito A es el número de elementos que tiene dicho
conjunto.
A ese número lo denotaremos por | A |. No es difícil llegar a que, si tenemos dos conjuntos A y B, entonces | A
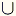 B | = | A | + | B | – | A B | = | A | + | B | – | A 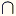 B | B |
Ejemplo:
Se sabe que, de los 65 alumnos del sexto curso, a 30 les gusta la Biología, a 40 las Matemáticas y a 10 les gustan ambas asignaturas. El diagrama de Venn que representa el enunciado es el que aparece a la derecha. Claramente, el conjunto universal debe ser U = {x / x es alumno del sexto curso}. Representemos por: B={x Entonces, según el enunciado, | U | = 65, | B | = 30, | M | = 40, | B Los números que aparecen en las regiones coloreadas corresponden a los cardinales de los conjuntos que representan. Así, | B
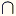 M| = 10, | B – M| = 30 – 10 = 20 y | M – B| = 40 – 10 = 30, M| = 10, | B – M| = 30 – 10 = 20 y | M – B| = 40 – 10 = 30,
El | B
El cardinal de (B |
|
|
|
|
Sonia Margarita Armas Gómez |
|
|
|
Ministerio de Educación, Cultura y Deporte. Año 2011 |
|
|
|
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.