 VECTORES-1
VECTORES-12º de Bachillerato de CNST (Geometría)
|
Recordemos que una pareja de números (x,y) designa un punto del
plano o un vector del mismo. De forma parecida, una terna (x,y,z)
va a ser entendida en primer lugar como una posición en el
espacio y después como un vector. En las siguientes escenas vamos a estudiar el espacio. En
lugar de los dos ejes de coordenadas tendremos tres. En la escena, sólo hemos dibujado la parte positiva de cada uno de ellos, el eje OX en rosa, el eje OY en verde y el eje OZ en amarillo. Si pulsas inicio, la escena se vacía y sólo quedarán los ejes. Puedes mover la escena con el ratón. Si se mueve muy rápido o quieres pararla, pulsa en cualquier lado una vez. También puedes pulsar inicio y empezar de nuevo siempre que lo desees. |
|
| Cuando hayas "mareado" bastante el espacio, aumenta los valores Xb, Yb y Zb que aparecen abajo. Son las coordenadas del punto B(Xb,Yb,Zb).Cuando quieras, haz lo mismo con las coordenadas de A(Xa,Ya,Za) | |
|
Comprueba que entiendes lo que ves,
en relación con las coordenadas de los puntos
A(Xa,Ya,Za) y
B(Xb,Yb,Zb) cuyas coordenadas aparecen abajo. Dichos puntos son
los extremos del vector fijo AB, que está dibujado en rojo. Sus
respectivas componentes tienen el mismo color que los ejes, y se
calculan restando las de B, punto final o extremo, menos las de
A,
punto origen o inicial: vector(AB)=(Xb-Xa,Yb-Ya,Zb-Za) Aparecen en la "pizarra" junto con el módulo del vector. Aplicando el teorema de Pitágoras,¿podrías confirmarlo en tus apuntes? (fíjate en el segmento azul, y mueve la escena hasta que lo consideres necesario) |
|
Puedes variar las coordenadas de A y de B y observar otros vectores fijos.
¿Qué sucede si coincide alguna coordenada de A con la respectiva de B?
2.Vectores fijos equipolentes. Vector libre.
| Cuando dos vectores AB y CD tienen las mismas coordenadas, se dice que son equipolentes. | |
| En esta escena, al dar al botón inicio, observas un único vector. Pero si alteras las coordenadas Xa, Ya y Za, observarás que se distingue el vector AB, en azul, de otro vector en rojo cuyo origen permanece en el origen de coordenadas (0,0,0) | |
|
En cuanto muevas la escena con el ratón, te darás cuenta que los
vectores azul y rojo tienen: - direcciones paralelas - el mismo sentido - el mismo módulo Si ahora pulsas sobre el botón que hay arriba "más vectores", verás aparecer, pues eso, más vectores equipolentes al vector azul AB. |
|
Todos los vectores fijos equipolentes entre sí definen al vector
libre, que se identifica por la terna de números que se obtiene al
restar las coordenadas del punto extremo menos las del punto inicial, o
sea: 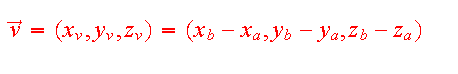
Por tanto, las coordenadas de un punto P(x,y,z) coinciden con las de su vector de posición OP, que es el vector cuyo inicio es el origen de coordenadas O(0,0,0) y cuyo final es dicho punto P.
3.Coordenadas de un vector libre.
| Una idea que nos vendrá bien consiste en entender un vector libre como una "idea" de movimiento, que no depende del punto inicial, pero que está caracterizada por una dirección de movimiento, un sentido del movimiento dentro de esa dirección y un tamaño, que viene dado por el módulo del vector. | |
|
Para entender las coordenadas del vector, la idea de movimiento del vector (x,y,z), es la secuenciación (suma) de los movimientos siguientes: - 1º, de (0,0,0) a (x,0,0), que sería la coordenada "x". Varía el control X, para que lo veas. - 2º, de (x,0,0) a (x,y,0), que sería la coordenada "y". Haz lo mismo con el control Y. - 3º, de (x,y,0) a (x,y,z), que sería la coordenada "z". Repite lo mismo con Z. Mueve la escena con el ratón las veces que lo consideres oportuno, e introduce los valores que quieras en los controles X, Y y Z, hasta que tengas claro lo que es un vector y lo que son sus coordenadas. |
|
|
|||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.