2. Semejanza: el Teorema de Tales

Se considera a Tales de Mileto el iniciador de la indagación racional sobre el universo. También se le considera el primer filósofo de la historia y el fundador de la escuela jonia de filosofıa, según el testimonio de Aristóteles.

Fue el primero y el más famoso de los siete sabios de Grecia (el sabio astrónomo) y tuvo como discıpulo y protegido a Pitágoras. Es, además, uno de los más grandes astrónomos y matemáticos de su época, hasta tal punto que era una lectura obligatoria para cualquier matemático de la Edad Media y Contemporánea. Sus estudios incidieron profúndamente en las áreas de la Geometrıa, Álgebra lineal, Geometrıa del Espacio y algunas rmas de la Fısica, tales como la Estática, Dinámica y Óptica. Su vida está envuelta en un halo de leyenda.

Este matemático enunción, en sus estudios acerca de la geometrıa, el Primer Teorema de Thales, el cual se puede encontrar enunciado en diferentes formas. Una de las más utilizadas, y la que expondremos aquı es la siguiente:

Teorema 1 (Primer Teorema de Tales)   Cuando dos rectas se cortan con varias lıneas paralelas se determinan segmentos proporcionales, y las figuras que se forman se dice que están en proporción de Tales.

Figure 2.1: Teorema de Tales

Si representamos gráficamente esta situación, como en el gráfico 2.1, las relaciones que se expresan en el Teorema de Tales son las siguientes:

$$\frac{DE}{AB} = \frac{EF}{BC}$$

Ejercicio 1   Utiliza el applet interactivo para comprobar que, bajo las condiciones expuestas en el problema, se verifica el teorema de Tales.

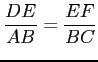El mismo teorema se puede reescribir utilizando triángulos, de la siguiente forma:

Teorema 2   En dos triángulos semejantes, los lados correspondientes son proporcionales.

Se suelen representar tales triángulos compartiendo un ángulo y haciendo coincidir los lados que determinan dicho ángulo. Se dice entonces que están en posición de Tales, como se ve en al figura 2.2

Figure 2.2: Triángulo en posición de Tales

Esta relación de proporcionalidad se puede expresar como la relación de igualdad:

$$\frac{\overline{AB}}{\overline{ab}} = \frac{\overline{BC}}{\overline{bc}} = \frac{\overline{CA}}{\overline{ca}}$$

de donde, despejando, se puede obtener fácilmente el siguiente conjunto de equivalencias:

$$\begin{aligned}\frac{\overline{AB}}{\overline{BC}} = \frac{\ove... ...overline{AC}} = \frac{\overline{ab}}{\overline{ac}} \end{aligned}$$

Estas equivalencias indican que las proporciones entre lados son constantes en triángulos semejantes, es decir, que la proporción que se establece entre dos lados de un triángulo vale lo mismo para cualquier triángulo semejante.

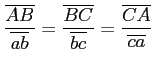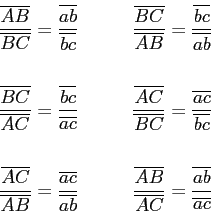Consideremos ahora triángulos rectángulos, esto es, que tienen un ángulo recto ($90^\circ$). Puesto que la suma de los ángulos de un triángulo es de $180^\circ$, los restantes ángulos no rectos tienen que sumar $90^\circ$, por lo que conocer uno de ellos determina, automáticamente la forma del triángulo al conocerse sus tres ángulos, como se indica en la figura 2.3. Por lo tanto, todos los triángulos rectángulos que tienen un ángulo no recto $\alpha$ son semejantes.

Figure 2.3:

Puesto que todos estos triángulos son semejantes, las proporciones variarán en función, no de la longitud de los lados, sino de la medida del ángulo $\alpha$:

Ejercicio 2   Utiliza el applet interactivo para comprobar que, bajo las condiciones expuestas en el problema, se verifica que las proporciones entre los lados del triángulo rectángulo dependen del ángulo $\alpha$, y no de las longitudes de los lados.

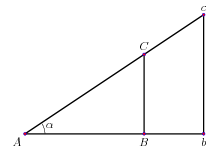
Una vez hayas comprobado esto, tiene sentido definir las razones trigonométricas.