Transformaciones de funciones: f(x)+a, f(x+b) 
Análisis
 
Transformación f(x) →f(x+b)

En este apartado veremos cómo queda transformada la gráfica de una función en la a la variable sumaremos un valor constante b.

Es decir vamos a comparar las gráficas de las funciones y=f(x) e y=f(x+b)

Igual que antes puedes modificar los valores de b, bien con pulsando las flechas azul (para aumentar) roja (para disminuir), o bien escribiendo directamente el valor que quieras y pulsando intro 

Prueba a dar al parámetro b los valores b=1, 3, -1, -2. 

Modifica los valores con los controles y observa lo que sucede

Se puede observar que la gráfica de la función se desplaza hacia la izquierda a unidades si a >0 y hacia la derecha a unidades si a<0 

Ejercicio 6: Dada la gráfica de la función y=x2 dibuja en tu cuaderno, de manera aproximada, las gráficas de las funciones  y=(x-1)2. y=(x+2)2

Ejercicio 7: Sabiendo que la gráfica de la función y=f(x) corta al eje OX en los puntos A(0,2) y B(0,5), calcular los puntos de corte de la función y=f(x-3)

Vamos a comprobar que efectivamente todos los puntos de la gráfica quedan desplazados a derecha o izquierda respecto de la gráfica original b unidades
Tienes dibujadas las gráficas de la función  y=f(x) e y=f(x+b) Modifica el valor de b y mira lo que le sucede a la gráfica
Mueve el punto que aparece en la gráfica de  y=f(x). Observa que la distancia entre los valores de f(x) y f(x+b) se corresponde con el valor que hayas elegido de b.

 

Ejercicio 8: Sea la función y=x2 . Se han coloreado los valores que están relacionados. Observa la tabla y compara los diferentes valores de la función ¿Qué conclusiones puedes sacar? Anota en tu cuaderno tus comentarios e intenta escribir una regla general
x -5 -4 -3 -2 -1  0  1  2  3  4   5
f(x)=x2 25 16 9 4 1 0 1 4 9 16 25
f(x+1)=(x+1)2  16 9   4  1  0 1 4 9 16 25 36
f(x-2)=(x+2)2 9 4  1  0  1 4 9 16 25 36 49

x -5 -4 -3 -2 -1  0  1  2  3  4   5
f(x)=x2 25 16 9 4 1 0 1 4 9 16 25
f(x+1)=(x-1)2  36 25 16 9 4 1 0 1 4 9 16
f(x-2)=(x-2)2 49 36 25 16 9 4 1 0 1 4 9


Composición de ambas transformaciones f(x) →f(x+b)+a

Vamos a trabajar ahora con las dos transformaciones que hemos visto hasta ahora. La primera de ellas, f(x)+a, nos trasladaba la gráfica hacia arriba o hacia abajo, mientras que f(x+b) nos la mueve a derecha o izquierda. Componiendo ambas podremos trasladar nuestra gráfica en cualquier dirección. Comprueba, moviendo el punto, que siempre existe la misma correspondencia entre un punto y el trasladado correspondiente.


 
Ejercicio 9:  A partir de la gráfica de la función y=cos(x), dibuja de manera aproximada, sin hacer ninguna tabla de valores, las gráficas de las funciones siguientes:
  • y=cos(x-2)+1
  • y=cos(x+3)-1
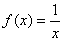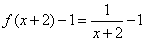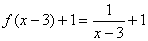Ejercicio 10: Dada la hipérbola Hipérbola dibujar en tu cuaderno ,de manera aproximada, las gráficas de las hipérbolas Hipérbola 2, Hipérbola3
Ejercicio 11: Vamos a aplicar lo que sabemos para dibujar las funciones del tipo 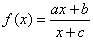Hipérbola 4. Lo veremos con un ejemplo.
Sea la función que queremos representar . Dividimos los polinomios del numerador y del denominador

  2x-1
x-1
-2x+2 2

1   

 

Ahora podemos escribir de donde deducimos que tendrá la misma gráfica que desplazada 1 unidad a la derecha y 2 arriba. Dibújala en tu cuaderno y repite el proceso con la función .

Puedes comprobar las soluciones de los ejercicios 9, 10 y 11 en la escena siguiente:
Introduce en la parte izquierda la función que tomas como inicial y en la parte derecha la modificada-desplazada y compara con lo que has dibujado en tu cuaderno




       
           
  Francisco Javier Medrano Sánchez
 
Ministerio de Educación, Cultura y Deporte. Año 2009