Los puntos de corte con los ejes coordenados son característicos y casi nunca renunciamos, cuando tenemos que esbozar la curva, a representarlos ya que son puntos de paso de una región a otra en el sistema de representación.

a) Corte con el eje OX: Estos puntos se caracterizan por que la ordenada es nula, y=0.

Para hallarlos resolvemos la ecuación f(x)=0. Hay tantos cortes como soluciones reales tenga la ecuación.

b) Corte con el eje OY: A lo más puede haber un corte. El punto de corte se caracteriza porque la abcisa es nula, x=0, y al sustituir este valor en la ecuación y=f(x) se obtiene y=f(0).

Si la función f(x) está definida para x=0, es decir 0 pertenece al dominio D_f, no puede existir más que un valor f(0) ya que la función es una correspondencia unívoca de D_f en R ( a cada valor del dominio solo le corresponde una imagen).

Si la función no está definida para x=0, no hay corte con el eje OY.

c) Regiones: Nos interesan las regiones de la función donde ésta es positiva, f(x)>0, o negativa f(x)<0

Cuando tenemos que representar la gráfica es de gran ayuda rayar las zonas donde no puede haber  representación y éstas estarán por encima o por debajo del eje OX, es decir donde f(x)>0 y f(x)<0 respectivamente.

Cuando cambia el signo de la función, está pasa por un corte en OX o por una discontinuidad.

El procedimiento para determinar estas regiones es el que sigue:

1º Hacemos una tabla con dos filas. En la primera representamos x , colocando ordenadamente: -¥, +¥ puntos de corte con OX y puntos de discontinuidad. En la segunda fila, debajo de esos puntos dibujamos una raya vertical.

2º En la segunda fila escribimos el signo que tiene f(x) en cada intervalo obtenido arriba. Para ello basta evaluar el signo de un punto cualquiera de cada intervalo.

En el programa siguiente puede comprobarse que con muy pocos elementos de cálculo, es posible orientar la forma gráfica de la función y hacer un esbozo de la misma.

La función que tomamos como modelo es la que se ha puesto de ejemplo después del estudio teórico hecho en la columna de la derecha.

En una presentación de 6 pasos obtenemos:

Paso nº 1: Puntos de discontinuidad.

Paso nº 2: Puntos de corte con el eje OX

Paso nº 3: Punto de corte con el eje OY

Paso nº 4: Regiones, donde f(x)>0 y f(x)<0

Paso nº 5: Ramas infinitas cuando x®± ¥ y cuando x®2⁺, x®2^-, x®-2⁺, x®-2^-. 

Paso nº 6: Esbozo de la gráfica.

Ejemplo:

Hallar las regiones de la función 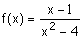, dibujando los puntos característicos: cortes con un punto lleno y discontinuidades con un punto hueco.

- Discontinuidades: x²-4=0 ® x=2, x=-2.

- Dominio: R - {-2,2}

- Cortes OX: f(x)=0 ® x-1=0 ® x=1

- Corte con OY: x=0 ® f(0)= 1/4

- Regiones:

Ejercicios: Dibujar los cortes con los ejes, las discontinuidades, las regiones, las ramas infinitas. Esbozar la gráfica. 

	Función	Expresión para el programa	solución
1		(2*x^2-5*x+2)/(x^2-2*x-3)
2		sqrt((x+3)/(x+2))

Resolver los ejercicios analíticamente y después utilizar el programa siguiente para verificar la solución, reemplazando la entrada editable f(x) por la expresión correspondiente.