Los decimales periódicos puros.
|
Números
decimales: Los decimales periódicos puros. |
| Álgebra | |
| Decimales periódicos puros. | |
|
Los decimales periódicos puros son aquellos en los que el periodo (es decir, la parte decimal que se repite) empieza justo después de la coma. Así, por ejemplo, 2/3=0'666666... De la misma forma que veíamos en los decimales periódicos puros, los peri
|
|
Para encontrar la fracción generatriz de un decimal
periódico puro podemos utilizar la siguiente fórmula: |
|
| Veamos algunos ejemplos de
fracción generatriz de un decimal periódico puro: Si queremos convertir el número  ,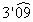
pensamos primero en que su periodo tiene 2 cifras decimales, así que el
numerador de la fracción sería el número sin comas (309) menos la parte
entera (3), es decir, 309-3=306. El denominador, al tener 2 cifras el
periodo, sería 99, con lo que la fracción generatriz de este decimal
sería 309/99.Estas fracciones, siempre que sea posible, podemos simplificarlas, dividiendo el denominador y el denominador por el máximo común divisor de éstos, para convertirla en irreducible. En nuestro ejemplo, m.c.d. (309,99)=3, con lo que, dividiendo numerador y denominador por 3, nos quedaría que la fracción generatriz es la fracción irreducible 103/33. |
|
|
|
Ejercicio
5: Calcula en tu cuaderno la fracción generatriz de los siguientes decimales periódicos puros, y luego comprueba el resultado con la escena de al lado:  |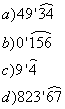
 |
 |
 |
||||
 |
| Isabel María Picón Jaramillo | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2009 | ||
Los
contenidos de esta unidad didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.
