
 |
La integral definida: método de exhaución |
| Análisis. | |
| Introducción . | ||||
|
Vamos a conocer este método basándonos en un ejemplo. Nuestro objetivo inicial será calcular el área del recinto plano limitado por el eje de abscisas, la gráfica de la función y = x2 y las rectas x = 0 y x = b, siendo b un número real cualquiera. Más concretamente, lo que queremos hallar es el área de la región coloreada en la figura siguiente:
El método de exhaución empleado por Arquímedes para resolver este mismo problema (aunque con notación más moderna) consiste en lo siguiente: Para cada número natural n dividimos el segmento [0,b] en n partes iguales de longitud b/n. Sobre cada una de esas partes construimos un rectángulo con la altura de la ordenada máxima (rectángulo superior, por exceso o circunscrito). | ||||
|
Realiza en la siguiente escena las actividades que se te proponen: | ||||
|
1.- Modifica los valores de n y de b para observar lo que se dice en el párrafo anterior. Si n es muy grande los rectángulos que aparecen tendrán una base muy pequeña y será difícil distinguirlos. Prueba en ese caso a modificar la escala o la posición de los ejes para mejorar su visualización. | ||||
|
2.- Para cada valor de n, llamaremos Sn (o suma superior) a la suma de las áreas de todos los rectángulos superiores. ¿Qué puedes afirmar de Sn en comparación con el valor del área que estamos buscando? ¿Es cierta esa afirmación sea cual sea el valor de n? | ||||
|
3.- Sean n1 y n2 dos posibles valores del parámetro n, y supongamos n1 < n2, ¿Qué puedes afirmar de los respectivos valores Sn1 y Sn2? | ||||
|
4.- Intenta dar un enunciado teórico que englobe los resultados de las dos cuestiones anteriores. | ||||
|
Ahora hacemos los mismo, construyendo rectángulos de altura la ordenada mínima (rectángulo inferior, por defecto o inscrito). | ||||
|
Realiza las actividades que se te proponen en la figura adjunta: | ||||
|
1.- Para cada valor de n, llamaremos sn (o suma inferior) a la suma de las áreas de todos los rectángulos inferiores. ¿Qué puedes afirmar de sn en comparación con el valor del área que estamos buscando? ¿Es cierta esa afirmación sea cual sea el valor de n? | ||||
|
2.- Sean n1 y n2 dos posibles valores del parámetro n, y supongamos n1 < n2, ¿Qué puedes afirmar de los respectivos valores sn1 y sn2? | ||||
|
3.- Intenta dar un enunciado teórico que englobe los resultados de las dos cuestiones anteriores. | ||||
|
Ahora las dos situaciones simultáneamente. | ||||
|
Realiza las actividades que se te proponen en la figura adjunta: | ||||
|
1.- ¿Qué relación hay entre cualquier "suma superior" Sn y cualquier "suma inferior" sm? | ||||
|
2.- Si llamamos A al área que queremos calcular, ¿qué relación hay entre A, Sn y sm ? | ||||
|
3.- ¿Qué puede decirse de Sn - sn cuando n tiende a infinito? | ||||
|
4.- Averigua el valor del área buscada inicialmente para distintos valores de b y con un error menor que una décima. | ||||
| José Luis Alonso Borrego | ||
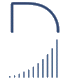 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.